题目内容
7.已知f(x)=-x+sinx,命题p:?x∈(0,$\frac{π}{2}$),f(x)<0,则( )| A. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | B. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | ||
| C. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | D. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 |
分析 利用导数可判定函数f(x)在x∈(0,$\frac{π}{2}$)上单调递减,即可判断出真假,再利用命题的否定可得¬p.
解答 解:f(x)=-x+sinx,?x∈(0,$\frac{π}{2}$),则f′(x)=cosx-1<0.
∴函数f(x)在x∈(0,$\frac{π}{2}$)上单调递减,∴f(x)<f(0)=0,
则命题p:?x∈(0,$\frac{π}{2}$),f(x)<0,为真命题.
¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0.
故选:D.
点评 本题考查了利用导数判定函数的单调性极值、复合命题真假的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.函数f(x)对任意的x∈R都有f(x)=f(2-x),且当x≠1时,其导函数f'(x)满足xf'(x)>f'(x),若1<a<2,则( )
| A. | f(2a)<f(2)<f(log2a) | B. | $f(2)<f({log_2}a)<f({2^a})$ | C. | $f({log_2}a)<f({2^a})<f(2)$ | D. | $f({log_2}a)<f(2)<f({2^a})$ |
15.在函数①y=|sinx|;②$y=tan\frac{x}{2}$;③y=|tanx|;④2y=cos|x|中,最小正周期为2π的所有函数为( )
| A. | ①②③④ | B. | ②③④ | C. | ②④ | D. | ①③ |
12.非常数数列{an}是等差数列,且{an}的第5、10、20项成等比数列,则此等比数列的公比为( )
| A. | $\frac{1}{5}$ | B. | 5 | C. | 2 | D. | $\frac{1}{2}$ |
19.如图,已知PA⊥平面ABC,∠ABC=120°,PA=AB=BC=6,$|{\overrightarrow{PC}}|$=等于( )
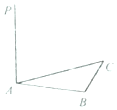

| A. | $6\sqrt{2}$ | B. | 6 | C. | 12 | D. | 144 |
 如图,边长为5的正方形ABCD与矩形ABEF所在平面互相垂直,M,N分别为AE,BC的中点,AF=4.
如图,边长为5的正方形ABCD与矩形ABEF所在平面互相垂直,M,N分别为AE,BC的中点,AF=4.