题目内容

4．函数f（x）=$\left\{\begin{array}{l}2x-{x^2}（0≤x≤3）\\{x^2}+6x（-2≤x＜0）\end{array}\right.$的值域是[-8，1]．

分析 分别根据定义域求解出函数的值域的并集，可得f（x）的值域范围．

解答 解：函数f（x）=$\left\{\begin{array}{l}2x-{x^2}（0≤x≤3）\\{x^2}+6x（-2≤x＜0）\end{array}\right.$，
当0≤x≤3时，f（x）=2x-x2=-（x-1）2+1，其值域为[-3，1]，
当-2≤x≤0时，f（x）=x2+6x=（x+3）2-9，其值域为[-8，0]
∴可得f（x）的值域范围是[-8，1]．
故答案为[-8，1]．

点评 本题主要考查了分段函数的值域的求法，要注意定义域的范围和单调性的运用．比较基础．

练习册系列答案
相关题目
14．若x，y满足约束条件$\left\{\begin{array}{l}2x+y≤8\\ x+3y≤9\\ x≥0，y≥0\end{array}\right.$，则$\frac{y-6}{x-6}$的最大值为3．
15．在函数①y=|sinx|；②$y=tan\frac{x}{2}$；③y=|tanx|；④2y=cos|x|中，最小正周期为2π的所有函数为（　　）
A．①②③④B．②③④C．②④D．①③
12．非常数数列{an}是等差数列，且{an}的第5、10、20项成等比数列，则此等比数列的公比为（　　）
A．$\frac{1}{5}$B．5C．2D．$\frac{1}{2}$
19．如图，已知PA⊥平面ABC，∠ABC=120°，PA=AB=BC=6，$|{\overrightarrow{PC}}|$=等于（　　）
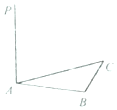
A．$6\sqrt{2}$B．6C．12D．144
9．已知函数f（x）是定义在R上的增函数，若f（a2-a）＞f（2a2-4a），则实数a的取值范围是（　　）
A．（-∞，0）B．（0，3）C．（3，+∞）D．（-∞，0）∪（3，+∞）
16．已知关于x的一元二次方程x2+2mx+2m+1=0有两个根，求满足下列条件的m的取值范围．
（1）两个根都小于0；
（2）其中一个根在区间（-1，0）内，另一个根在区间（1，2）内．
13．下列命题中正确的是（　　）
A．若命题p为真命题，命题q为假命题，则命题“p且q”为真命题
B．“$sinα=\frac{1}{2}$”是“$α=\frac{π}{6}$”的充分不必要条件
C．l为直线，α，β，为两个不同的平面，若l⊥α，α⊥β，则l∥β
D．命题“?x∈R，2x＞0”的否定是“?x0∈R，${2^{x_0}}$≤0”
14．函数f（x）=x3+x的奇偶性是（　　）
A．偶函数B．奇函数C．非奇非偶D．无法判断

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网