题目内容

已知{an}为等差数列，Sn为其前n项和，且a3=9，S6=60．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足b1=1，bn+1=abn，求数列{bn}的前n项和Tn
（Ⅲ）若
7
m
35
≤
1
2n+3
（1+
1
a1
）（1+
1
a2
）…（1+
1
an-1
）对n≥2且n∈N*恒成立，求实数m的最大值．
考点：数列与不等式的综合,数列的求和
专题：新定义,等差数列与等比数列,不等式的解法及应用
分析：（Ⅰ）本题先利用等差数列的通项公式求出其首项和公差，得到等差数列的通项公式；（Ⅱ）再利用（1）的结论，结合新数列的定义，求出新的数列的通项公式；（Ⅲ）利用n的代数式的单调性，求出相应式子的最值，得到本题结论．
解答： 解：（I）由已知得
a1+2d=9
6a1+
6×5×d
2
=60
，
解得
a1=5
d=2
，
∴an=2n+3．
（II）∵an=2n+3，
∴bn+1=2bn+3，
∴bn+1+3=2（bn+3），
又b1+3=4，
∴{bn+3}是以4为首项2为公比的等比数列．
∴bn+3=4•2n-1，bn=2n+1-3．
∴Tn=
4•(1-2n)
1-2
-3n=2n+2-3n-4．
（Ⅲ）设An=(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
7
m
35
≤(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
7
m
35
≤(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
7
m
35
≤(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
…
7
m
35
≤(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
，
则当n≥2且n∈N*时，
An+1
An
=
(1+
1
a1
)•(1+
1
a2
)…(1+
1
an
)•
1
2n+5
(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
1
2n+5
(1+
1
a1
)(1+
1
a2
)…(1+
1
an
)
1
2n+3
(1+
1
a1
)(1+
1
a2
)…(1+
1
an-1
)
=
2n+3
(1+
1
an
)
2n+5

=
2n+4
2n+3
•
2n+3
2n+5
=
2n+4
(2n+3)(2n+5)
=
2n+4
4n2+16n+15
＞
2n+4
4n2+16n+16
=1=
4n2+16n+16
4n2+16n+15
＞1．
所以An+1＞An，即当n增大时，An也增大．
要使
7
m
35
≤(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
≤
7
m
35
≤(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
7
m
35
≤(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
7
m
35
≤(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
…
7
m
35
≤(1+
1
a1
)•(1+
1
a2
)…(1+
1
an-1
)•
1
2n+3
对n≥2且n∈N*恒成立，
只需
7
m
35
≤(An)min即可．
∵(An)min=A2=
6
5
•
1
7
=
6
7
35
．
∴
7
m
35
≤
6
7
35
，即m≤6，
所以实数m的最大值为6．
点评：本题考查了等差数列通项公式的直接运用和技巧性运用，还利用单调性对数列相关最值进行研究，有一定的难度，属于难题．
练习册系列答案
相关题目
已知函数f（x）=sin2xcosφ+cos2xsinφ，x∈R，0＜φ＜π，f（
π
4
）=-
3
2
．
（1）求f（x）的表达式；
（2）若f（
α
2
-
π
3
）=
5
13
，α∈（
π
2
，π），求cosα的值．
已知函数f（x）=x-sinx-
1
3
ax3，其中a∈R．
（1）当a=1时，求函数g（x）=f（x）+sinx的极值；
（2）当a＜0时，证明：函数f（x）在R是单调函数．
已知函数f（x）=2sinxcosx+2
3
cos2x-
3
，x∈R．
（Ⅰ）求函数y=f（-3x）+1的最小正周期和单调递减区间；
（Ⅱ）已知△ABC中的三个内角A，B，C所对的边分别为a，b，c，若锐角A满足f（
A
2
-
π
6
）=
3
，且a=7，sinB+sinC=
13
3
14
，求△ABC的面积．
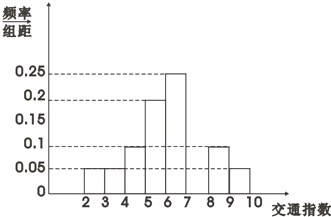交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为T．其范围为[0，10]，分别有五个级别：T∈[0，2）畅通；T∈[2，4）基本畅通； T∈[4，6）轻度拥堵； T∈[6，8）中度拥堵；T∈[8，10]严重拥堵，晚高峰时段（T≥2），从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制的部分直方图如图所示．
（Ⅰ）请补全直方图，并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个？
（Ⅱ）用分层抽样的方法从交通指数在[4，6），[6，8），[8，l0]的路段中共抽取6个路段，求依次抽取的三个级别路段的个数；
（Ⅲ）从（Ⅱ）中抽出的6个路段中任取2个，求至少一个路段为轻度拥堵的概率．
欧阳修《卖油翁》中写到：（翁）乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿．可见“行行出状元”，卖油翁的技艺让人叹为观止．若铜钱是直径为4cm的圆，中间有边长为1cm的正方形孔，若随机向铜钱上滴一滴油（油滴是直径为0.2cm的球）正好落人孔中的概率是
 
．
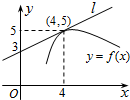如图，y=f（x）是可导函数，直线l是曲线y=f（x）在x=4处的切线，令g（x）=
f(x)
x
，则g′（4）=
 
．
定义：如果对任意一个三角形，只要它的三边长a，b，c都在函数f（x）的定义域内，就有f（a），f（b），f（c）也是某个三角形的三边长，则称f（x）为“保三角形函数”．若函数h（x）=lnx（x∈[M，+∞））是保三角形函数，求M的最小值为
 
．
将编号为1，2，3，4的四个小球放到三个不同的盒子里，每个盒子至少放一个小球且编号为1，2的两个小球不能放到同一个盒子里，则不同放法的种数有
 
．（用数字作答）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网