题目内容
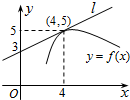如图，y=f（x）是可导函数，直线l是曲线y=f（x）在x=4处的切线，令g（x）=| f(x) |
| x |
考点：导数的运算
专题：导数的概念及应用
分析：先从图中求出切线过的点，利用导数在切点处的导数值为斜率得到切线的斜率，最后结合导数的几何意义求出f′（4）的值，
由g（x）=
，则g′（x）=
，进而得到g′（4）．
由g（x）=
| f(x) |
| x |
| xf′(x)-f(x) |
| x2 |
解答：
解：由图知，切线过（0，3）、（4，5），
∴直线l的斜率为
=
，
由于曲线在切点处的导数值为曲线的切线的斜率，
所以f′（4）=
，f（4）=5．
令g（x）=
，则g′（x）=
故g′（4）=
=-
故答案为：-
∴直线l的斜率为
| 5-3 |
| 4-0 |
| 1 |
| 2 |
由于曲线在切点处的导数值为曲线的切线的斜率，
所以f′（4）=
| 1 |
| 2 |
令g（x）=
| f(x) |
| x |
| xf′(x)-f(x) |
| x2 |
故g′（4）=
4×
| ||
| 42 |
| 3 |
| 16 |
故答案为：-
| 3 |
| 16 |
点评：解决有关曲线的切线问题常考虑导数的几何意义：曲线在切点处的导数值为曲线的切线的斜率．
练习册系列答案
相关题目