题目内容
已知Sn是数列{an}的前n项和,且满足Sn2=n2an+Sn-12(n≥2,n∈N+)又已知a1=0,an≠0,n=2,3,4…
(1)计算a2,a3,并求数列{a2n}的通项公式;
(2)若bn=(
)an,Tn为数列{bn}的前n项和,求证:Tn<
.
(1)计算a2,a3,并求数列{a2n}的通项公式;
(2)若bn=(
| 1 |
| 2 |
| 7 |
| 4 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由Sn2=n2an+Sn-12(n≥2,n∈N+),a1=0,an≠0,分别取n=2,3即可得出a2,a3.由Sn2=n2an+Sn-12,利用an=Sn-Sn-1,可得Sn+Sn-1=n2,利用递推式可得an+1+an=2n+1,变形为an+1-(n+1)=-(an-n),利用等比数列的通项公式即可得出an,进而得到a2n.
(2)由(1)可知:an=
.可得T2k=1+[(
)1+(
)3+…+(
)2k-3]+[(
)4+(
)6+…+(
)2k+2],利用等比数列的前n项和公式即可得出.即可证明.
(2)由(1)可知:an=
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
(1)解:∵Sn2=n2an+Sn-12(n≥2,n∈N+),a1=0,an≠0,
∴取n=2可得:
=22a2+
,即(0+a2)2=4a2+0,解得a2=4.
同理取n=3时可得:a3=1.
由Sn2=n2an+Sn-12,可得Sn2=n2(Sn-Sn-1)+Sn-12,
化为(Sn-Sn-1)(Sn+Sn-1-n2)=0,
∴Sn+Sn-1=n2.
∴Sn+1+Sn=(n+1)2,
∴an+1+an=2n+1,
化为an+1-(n+1)=-(an-n),
∴数列{an-n}是从第二项开始为等比数列,公比为-1,首项为a2-2=2.
∴an-n=2×(-1)n-2,
∴an=n+2(-1)n-2,
∴a2n=2n+2,
∴数列{a2n}的通项公式为a2n=2n+2.
(2)证明:由(1)可知:an=
n∈N*.
∴T2k=1+[(
)1+(
)3+…+(
)2k-3]+[(
)4+(
)6+…+(
)2k+2]
=1+
+
<1+
+
<
.
而T2k-1<T2k,
因此对于?n∈N*,Tn<
.
∴取n=2可得:
| S | 2 2 |
| S | 2 1 |
同理取n=3时可得:a3=1.
由Sn2=n2an+Sn-12,可得Sn2=n2(Sn-Sn-1)+Sn-12,
化为(Sn-Sn-1)(Sn+Sn-1-n2)=0,
∴Sn+Sn-1=n2.
∴Sn+1+Sn=(n+1)2,
∴an+1+an=2n+1,
化为an+1-(n+1)=-(an-n),
∴数列{an-n}是从第二项开始为等比数列,公比为-1,首项为a2-2=2.
∴an-n=2×(-1)n-2,
∴an=n+2(-1)n-2,
∴a2n=2n+2,
∴数列{a2n}的通项公式为a2n=2n+2.
(2)证明:由(1)可知:an=
|
∴T2k=1+[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=1+
| ||||
1-
|
| ||||
1-
|
| 2 |
| 3 |
| 1 |
| 12 |
| 7 |
| 4 |
而T2k-1<T2k,
因此对于?n∈N*,Tn<
| 7 |
| 4 |
点评:本题考查了递推式的应用、等比数列的定义及其通项公式及其前n选和公式,考查了分类讨论思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知F1,F2是椭圆和双曲线的公共焦点,M是它们的一个公共点,且∠F1MF2=
,则椭圆和双曲线的离心率的倒数之和的最大值为( )
| π |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
| D、4 |
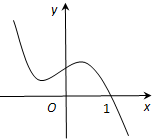
已知函数y=f(x)的图象如图,则满足f(
)•f(5)≤0的x取值范围为( )
| 2x+1 |
| x-1 |

| A、[-2,1) |
| B、[-1,1] |
| C、[1,2] |
| D、[2,3] |
设{an}是由正数组成的等比数列,Sn为其前n项和.已知a2a4=1,S3=7,则S5=( )
A、
| ||
B、
| ||
C、
| ||
D、
|