题目内容
求证:4sinθ(
-sin2θ)=4sinθ(
cos2θ-
sin2θ)
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
考点:三角函数恒等式的证明
专题:证明题,三角函数的求值
分析:对等式的左边运用同角的基本关系式的平方关系:cos2θ+sin2θ=1,即可得到右边.
解答:
证明:4sinθ(
-sin2θ)=4sinθ[
(cos2θ+sin2θ)-sin2θ]
=4sinθ(
cos2θ+
sin2θ-sin2θ)
=4sinθ(
cos2θ-
sin2θ),
则等式成立.
| 3 |
| 4 |
| 3 |
| 4 |
=4sinθ(
| 3 |
| 4 |
| 3 |
| 4 |
=4sinθ(
| 3 |
| 4 |
| 1 |
| 4 |
则等式成立.
点评:本题考查三角函数的证明,考查同角的平方关系的运用,属于基础题.

练习册系列答案
相关题目
已知全集U=R,A={x|y=
},则∁UA=( )
| 1 | ||
|
| A、[1,+∞) |
| B、(-∞,1) |
| C、(1,+∞) |
| D、(-∞,1] |
已知R是实数集,集合P={x|x2+2012x-2013>0},Q={y|y=
},则(∁RP)∩Q=( )
| -x2+2x+3 |
| A、(0,1] |
| B、[0,1] |
| C、(-1,1] |
| D、[-1,1] |
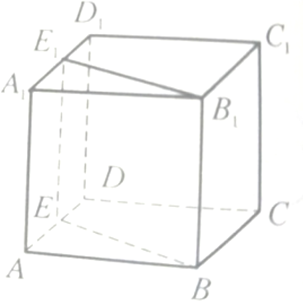 经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面AA1D1D于E1E.求证:BB1∥E1E.
经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面AA1D1D于E1E.求证:BB1∥E1E.