题目内容
已知θ为钝角,且sinθ=
,则tan
=( )
| ||
| 2 |
| θ |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点:同角三角函数基本关系的运用,半角的三角函数
专题:三角函数的求值
分析:根据同角的三角函数的关系即可得到结论.
解答:
解:∵θ为钝角,且sinθ=
,
∴cosθ=-
,
则tan
=
=
=
,
或者:由θ为钝角,且sinθ=
,得到θ=
,
则
=
,
则tan
=tan
=
,
故选:D
| ||
| 2 |
∴cosθ=-
| 1 |
| 2 |
则tan
| θ |
| 2 |
| sinθ |
| 1+cosθ |
| ||||
1-
|
| 3 |
或者:由θ为钝角,且sinθ=
| ||
| 2 |
| 2π |
| 3 |
则
| θ |
| 2 |
| π |
| 3 |
则tan
| θ |
| 2 |
| π |
| 3 |
| 3 |
故选:D
点评:本题主要考查三角函数值的计算,根据同角的三角函数的关系式是解决本题的关键.

练习册系列答案
相关题目
已知R是实数集,集合P={x|x2+2012x-2013>0},Q={y|y=
},则(∁RP)∩Q=( )
| -x2+2x+3 |
| A、(0,1] |
| B、[0,1] |
| C、(-1,1] |
| D、[-1,1] |
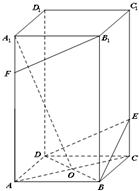 如图,在正四棱柱ABCD-A1B1C1D1中,点O是正方形ABCD对角线的交点,AA1=4,AB=2,点E,F分别在CC1和A1A上,且A1F=CE
如图,在正四棱柱ABCD-A1B1C1D1中,点O是正方形ABCD对角线的交点,AA1=4,AB=2,点E,F分别在CC1和A1A上,且A1F=CE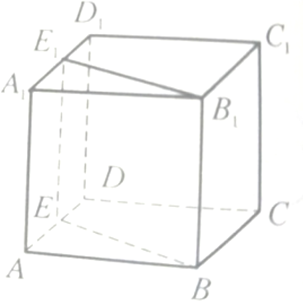 经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面AA1D1D于E1E.求证:BB1∥E1E.
经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面AA1D1D于E1E.求证:BB1∥E1E. 一个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得该几何体的体积是
一个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得该几何体的体积是