题目内容
 如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿边AB折起,使得△ABD与△ABC成30°的二面角D-AB-C,如图二,在二面角D-AB-C中.
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿边AB折起,使得△ABD与△ABC成30°的二面角D-AB-C,如图二,在二面角D-AB-C中.(1)求D、C之间的距离;
(2)求CD与面ABC所成的角的大小;
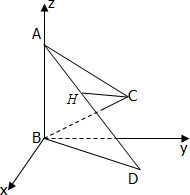
(3)求证:对于AD上任意点H,CH不与面ABD垂直.
考点:直线与平面所成的角,直线与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离,空间向量及应用
分析:(1)依题意建立空间直角坐标系使得△ABC在yoz平面上,由已知条件分别求出点C和点D的空间坐标,利用空间两点间的距离公式能求出D、C之间的距离.
(2)由题设条件求出面ABC的一个法向量和向量
,利用向量法能求出CD与平面ABC所成的角.
(3)
=t
,假设
⊥
,求出t的值,而此时CH和BD不垂直,CH不可能同时垂直BD和BA,问题得以证明
(2)由题设条件求出面ABC的一个法向量和向量
| CD |
(3)
| AH |
| AB |
| CH |
| BA |
解答:
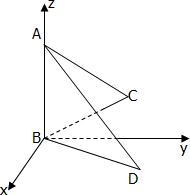 解:(1)依题意,∠ABD=90°,建立如图的坐标系使得△ABC在yoz平面上,
解:(1)依题意,∠ABD=90°,建立如图的坐标系使得△ABC在yoz平面上,
∵△ABD与△ABC成30°的二面角,∴∠DBY=30°,
又AB=BD=2,∴A(0,0,2),B(0,0,0),
C(0,
,1),D(1,
,0),
|CD|=
=
,
(2)∵x轴与面ABC垂直,∴(1,0,0)是面ABC的一个法向量.
设CD与面ABC成的角为θ,
∵
=(1,0,-1),
∴sinθ=
=
.
∵θ∈[0,
],∴θ=
;
∴CD与平面ABC的所成角是
.
(3)设
=t
=t(1,
,-2)=(t,
t,-2t),
∴
=
+
=(0,-
,1)+(t,
t,-2t)=(t,
t-
,-2t+1),
若
⊥
,则(t,
t-
,-2t+1)•(0,0,2)=0,
解得t=
,
∴此时
=(
,-
,0)
∵
=(1,
,0),
∴
•
=
-
=-1≠0,
∴CH和BD不垂直,
即CH不可能同时垂直BD和BA,
即对于AD上任意点H,CH不与面ABD垂直.
 解:(1)依题意,∠ABD=90°,建立如图的坐标系使得△ABC在yoz平面上,
解:(1)依题意,∠ABD=90°,建立如图的坐标系使得△ABC在yoz平面上,∵△ABD与△ABC成30°的二面角,∴∠DBY=30°,
又AB=BD=2,∴A(0,0,2),B(0,0,0),
C(0,
| 3 |
| 3 |
|CD|=
| 12+02+(-1)2 |
| 2 |
(2)∵x轴与面ABC垂直,∴(1,0,0)是面ABC的一个法向量.
设CD与面ABC成的角为θ,
∵
| CD |
∴sinθ=
| |(1,0,0)•(1,0.-1)| | ||||
|
| ||
| 2 |
∵θ∈[0,
| π |
| 2 |
| π |
| 4 |
∴CD与平面ABC的所成角是
| π |
| 4 |

(3)设
| AH |
| AB |
| 3 |
| 3 |
∴
| CH |
| CA |
| AH |
| 3 |
| 3 |
| 3 |
| 3 |
若
| CH |
| BA |
| 3 |
| 3 |
解得t=
| 1 |
| 2 |
∴此时
| CH |
| 1 |
| 2 |
| ||
| 2 |
∵
| BD |
| 3 |
∴
| CH |
| BD |
| 1 |
| 2 |
| 3 |
| 2 |
∴CH和BD不垂直,
即CH不可能同时垂直BD和BA,
即对于AD上任意点H,CH不与面ABD垂直.
点评:本题考查空间两点间的距离的求法,直线与平面所成角的大小的求法,线面垂直的判定定理,解题时要恰当地建立空间直角坐标系,用向量法求解,属于中档题

练习册系列答案
相关题目
已知不平行于坐标轴的直线l与以原点O为中心的双曲线
-
=1(a>0,b>0)的两 及其两条渐近线从左到右依次交于A,B,C,D不同的四点,则下列一定成立的是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、|AD|=2|BC| | ||||||||
| B、|AB|=|BC|=|CD| | ||||||||
C、
| ||||||||
D、
|
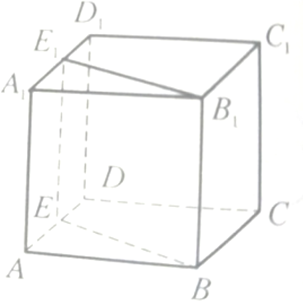 经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面AA1D1D于E1E.求证:BB1∥E1E.
经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面AA1D1D于E1E.求证:BB1∥E1E.