题目内容
已知数列{an}的通项公式an=2n•sin(
-
)+
ncos
,前n项和为Sn,则S2013= .
| nπ |
| 2 |
| π |
| 3 |
| 3 |
| nπ |
| 2 |
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:展开两角差的正弦化简,得到数列的所有偶数项为0,当n为4k+1,k∈N时,an=n;当n为4k+3,k∈N时,an=-n.分组后利用等差数列的前n项和得答案.
解答:
解:an=2n•sin(
-
)+
ncos
=2n(sin
•cos
-cos
•sin
)+
ncos
=2n(
sin
-
cos
)+
ncos
=nsin
.
∴当n为偶数时,an=0;
当n为4k+1,k∈N时,an=n;
当n为4k+3,k∈N时,an=-n.
则S2013=a1+a2+a3+…+a2013=(1+5+9+…+2013)-(3+7+9+…+2011)=
-
=1007.
故答案为:1007.
| nπ |
| 2 |
| π |
| 3 |
| 3 |
| nπ |
| 2 |
=2n(sin
| nπ |
| 2 |
| π |
| 3 |
| nπ |
| 2 |
| π |
| 3 |
| 3 |
| nπ |
| 2 |
=2n(
| 1 |
| 2 |
| nπ |
| 2 |
| ||
| 2 |
| nπ |
| 2 |
| 3 |
| nπ |
| 2 |
=nsin
| nπ |
| 2 |
∴当n为偶数时,an=0;
当n为4k+1,k∈N时,an=n;
当n为4k+3,k∈N时,an=-n.
则S2013=a1+a2+a3+…+a2013=(1+5+9+…+2013)-(3+7+9+…+2011)=
| (1+2013)×504 |
| 2 |
| (3+2011)×503 |
| 2 |
故答案为:1007.
点评:本题考查了两角和与差的正弦,考查了数列的求和,关键是对数列的项的规律的发现,是中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
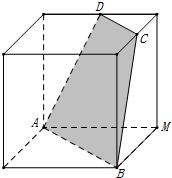 如图,正方体的棱长是a,C,D分别是两条棱的中点.
如图,正方体的棱长是a,C,D分别是两条棱的中点. 如图,四边形ABCD中,AD与BC不平行,
如图,四边形ABCD中,AD与BC不平行,