题目内容
已知椭圆
+
=1,直线y=x+m交椭圆于A,B,求S△AOB的最大值.
| x2 |
| 16 |
| y2 |
| 4 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:联立方程组得到方程5x2+8mx+4m2-16=0,求出x1+y2=-
,x1x2=
,从而求出|AB|的长,求出原点O到直线y=x+m的距离d,从而求出三角形的面积的最大值.
| 8m |
| 5 |
| 4m2-16 |
| 5 |
解答:
解:联立
,得:5x2+8mx+4m2-16=0,
△>0,设A(x1,y1),B(x2,y2),
x1+y2=-
,x1x2=
,
|AB|=
=
,
原点O到直线y=x+m的距离d=
,
∴S△AOB=
•
•
=
•
=
•
,
∴S△AOB的最大值是2
.
|
△>0,设A(x1,y1),B(x2,y2),
x1+y2=-
| 8m |
| 5 |
| 4m2-16 |
| 5 |
|AB|=
(-
|
4
| ||
| 5 |
原点O到直线y=x+m的距离d=
| |m| | ||
|
∴S△AOB=
| 1 |
| 2 |
| |m| | ||
|
4
| ||
| 5 |
| ||
| 5 |
| -m4+20m2 |
| ||
| 5 |
| -(m2-10)2+100 |
∴S△AOB的最大值是2
| 2 |
点评:考查三角形面积的最大值的求法,解题时要认真审题,注意椭圆弦长公式和二次函数性质的灵活运用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
设集合U={1,3,5,7},M={1,5},则∁UM=( )
| A、U | B、{1,7} |
| C、{3,7} | D、{5,7} |
关于曲线C:
+
=1,下列四个命题中,所有真命题的组合是( )
①曲线C上的横、纵坐标的取值范围分别是-5≤x≤5,-4≤y≤4;
②曲线C关于x轴、y轴都是对称的,还关于原点对称;
③设P,Q是曲线C上的任意两点,则|PQ|≤10恒成立;
④设M(-3,0),N(3,0),P是曲线C上任意的点,则|PM|+|PN|≤10恒成立.
| |x| |
| 5 |
| |y| |
| 4 |
①曲线C上的横、纵坐标的取值范围分别是-5≤x≤5,-4≤y≤4;
②曲线C关于x轴、y轴都是对称的,还关于原点对称;
③设P,Q是曲线C上的任意两点,则|PQ|≤10恒成立;
④设M(-3,0),N(3,0),P是曲线C上任意的点,则|PM|+|PN|≤10恒成立.
| A、①②③④ | B、①②③ |
| C、①②④ | D、①② |
| ∫ | 2 0 |
| 4-x2 |
| A、π | B、-π |
| C、π+2 | D、-π-2 |
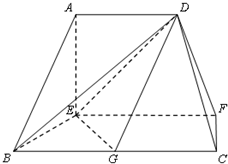 在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF∥BC,BC=2AD=4,AE=BE=2,G是BC的中点.
在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF∥BC,BC=2AD=4,AE=BE=2,G是BC的中点.