题目内容
已知O是坐标原点,点A(-1,0),若M(x,y)为平面区域
上的一个动点,则 |
+
|的取值范围是( )
|
| OA |
| OM |
A、[1,
| ||
B、[2,
| ||
| C、[1,2] | ||
D、[0,
|
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:作平面区域,求出向量OA,OM的和,以及模,通过图象观察当M与B重合时,取最小;当M与D重合时,取最大,代入计算即可得到范围.
解答:
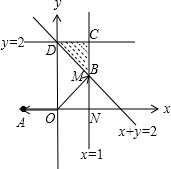 解:由约束条件
解:由约束条件
,作平面区域如图,
∵A(-1,0),M(x,y),
∴
+
=(-1,0)+(x,y)=(x-1,y),
则|
+
|=
.
由图可知,当M与B重合时,取最小,联立
,得B(1,1).
∴|
+
|的最小值是1.
当M与D重合时,取最大,代入点(0,2),可得最大为
.
则取值范围是[1,
].
故选A.
 解:由约束条件
解:由约束条件
|
∵A(-1,0),M(x,y),
∴
| OA |
| OM |
则|
| OA |
| OM |
| (x-1)2+y2 |
由图可知,当M与B重合时,取最小,联立
|
∴|
| OA |
| OB |
当M与D重合时,取最大,代入点(0,2),可得最大为
| 5 |
则取值范围是[1,
| 5 |
故选A.
点评:本题考查了简单的线性规划,考查了数形结合、转化与化归等解题思想方法,考查了向量模的求法,是中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
设
,
的夹角为θ,若||
|-|
||=|
+
|,则( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、cosθ=-1 |
| B、cosθ=1 |
| C、-1<cosθ<0 |
| D、0<cosθ<1 |
若a=20.5,b=logπ3,c=ln
,则( )
| 1 |
| 3 |
| A、b>c>a |
| B、b>a>c |
| C、a>b>c |
| D、c>a>b |
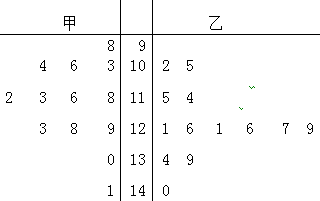
 一次学科测试成绩的频率分布直方图都受到不同程度的污损,可见部分如图.已知50~60分的有两个数,60~70分的有7个数,70~80分的有10个数,
一次学科测试成绩的频率分布直方图都受到不同程度的污损,可见部分如图.已知50~60分的有两个数,60~70分的有7个数,70~80分的有10个数,