题目内容

设
a 
，  
b 
的夹角为θ，若||
a
|-|
b
||=|
a
+
b
|，则（　　）
A、cosθ=-1
B、cosθ=1
C、-1＜cosθ＜0
D、0＜cosθ＜1
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：将所给的等式两边平方，再由向量的数量积的定义和性质，即可得到．
解答： 解：由于||
a
|-|
b
||=|
a
+
b
|，
则两边平方得，
a
2+
b
2-2|
a
|•|
b
|=
a
2+
b
2+2
a
•
b
，
则有
a
•
b
=-|
a
|•|
b
|=|
a
|•|
b
|cosθ，
即有cosθ=-1，
故选A．
点评：本题考查平面向量的运用，考查向量的数量积的定义，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知集合M={（x，y）|0≤y≤
4-x2
，且x+y-2≤0}，
（Ⅰ）在坐标平面内作出集合M所表示的平面区域；
（Ⅱ）若点P（x，y）∈M，求
y-3
3+x
的取值范围．
已知二次函数f（x）=-x2+bx（（b为常数）满足条件：方程f（x）=2x有两个相等的实数根．
（1）求f（x）的解析式；
（2）是否存在实数m，n（m＜n），使f（x）的定义域和值域分别为[m，n]和[4m，4n]？如果存在，请求出来．
已知椭圆
x2
25
+
y2
16
=1上的点P到椭圆一个焦点的距离为7，则P到另一焦点的距离为（　　）
A、2B、3C、5D、7
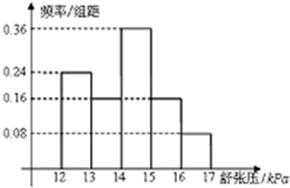为研究某药物的疗效，选取若干志愿者进行临床研究所有志愿者舒张压数据（单位：kPa）的分组区[12，13），[13，14），[14，15﹚，[15，16﹚，[16，17﹚，将其从左到右的顺序分别编号为第一组，第二组，…第五组，如图是根据试验数据组成的频率分布直方图，已知第一组与第二组共20人，第三组中没有疗效的有6人，则第三组的人数为
 
．
用列举法表示：大于0且不超过6的全体偶数的集合A=
 
．
已知O是坐标原点，点A（-1，0），若M（x，y）为平面区域
x+y≥2
x≤1
y≤2
上的一个动点，则 |
OA
+
OM
|的取值范围是（　　）
A、[1，
5
]
B、[2，
5
]
C、[1，2]
D、[0，
5
]
已知A={x∈N|x≤5}，B={x∈N|x＞1}，则A∩B=
 
．
已知圆锥的侧面展开图是面积为2π的半圆面，则该圆锥的体积为（　　）
A、
2
3
3
π
B、
2
2
3
π
C、
3
3
π
D、
2
3
π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网