已知i为虚数单位.则其连续2017个正整数次幂之和i+i2+i3+-+i2017=i．题目和参考答案——青夏教育精英家教网—

题目内容

12．已知i为虚数单位，则其连续2017个正整数次幂之和i+i²+i³+…+i²⁰¹⁷=i．

分析利用复数的周期性、等比数列的求和公式即可得出．

解答解：∵i⁴=1，∴i²⁰¹⁷=（i⁴）⁵⁰⁴•i=i．
∴i+i²+i³+…+i²⁰¹⁷=$\frac{i（{1-i}^{2017}）}{1-i}$=$\frac{i（1-i）}{1-i}$=i．
故答案为：i．

点评本题考查了复数的周期性、等比数列的求和公式，考查了推理能力与计算能力，属于基础题．

练习册系列答案

相关题目

6a²

4a²

$\frac{{\sqrt{3}}}{4}{a^2}$

D．

$\sqrt{3}{a^2}$

3．设定义域为R的奇函数$f（x）=\frac{1}{{{2^x}+a}}-\frac{1}{2}$（a为实数）．
（Ⅰ）求a的值；
（Ⅱ）判断f（x）的单调性（不必证明），并求出f（x）的值域；
（Ⅲ）若对任意的x∈[1，4]，不等式f（k-$\frac{2}{x}$）+f（2-x）＞0恒成立，求实数k的取值范围．

20．

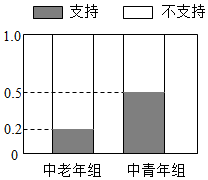国家实施二孩放开政策后，为了了解人们对此政策持支持态度是否与年龄有关，计生部门将已婚且育有一孩的居民分成中老年组（45岁以上，含45岁）和中青年组（45岁以下，不含45岁）两个组别，每组各随机调查了50人，对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图，如图所示：

	支持	不支持	合计
中老年组	10	40	50
中青年组	25	25	50
合计	35	65	100

（1）根据以上信息完成2×2列联表；
（2）是否有99%以上的把握认为人们对此政策持支持态度与年龄有关？

P（K²≥k₀）	0.050	0.010	0.001
k₀	3.841	6.635	10.828

附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．

7．执行如图所示的程序，若输出的结果为2，则输入的x的值为（　　）

17．某品牌电脑专卖店的年销售量y与该年广告费用x有关，如表收集了4组观测数据：

x（万元）	1	4	5	6
y（百台）	30	40	60	50

以广告费用x为解释变量，销售量y为预报变量对这两个变量进行统计分析．
（1）已知这两个变量呈线性相关关系，试建立y与x之间的回归方程$\hat y=\hat bx+\hat a$；
（2）假如2017年该专卖店广告费用支出计划为10万元，请根据你得到的模型，预测这一年的销售量y．
参考公式：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．

4．已知集合M={y|y=-x²+4}，N={x|y=log₂x}，则M∩N=（　　）

1．已知$cos（x-\frac{π}{4}）=\frac{{\sqrt{2}}}{10}，x∈（\frac{π}{2}，\frac{3π}{4}）$．
（1）求sinx的值；
（2）求$sin（2x+\frac{π}{6}）$的值．

2．命题：“?x＞0，x²+x≥0”的否定形式是（　　）

?x₀＞0，x₀²+x₀＜0

?x₀≤0，x₀²+x₀＞0

试题分类