题目内容
已知函数f(x)=log
为奇函数
(1)求常数k的值;
(2)设h(x)=
,证明函数y=h(x)在(1,+∞)上是减函数;
(3)若函数g(x)=f(x)-(
)x+m,且g(x)在区间[3,4]上没有零点,求实数m的取值范围.
| 1 |
| 2 |
| 1-kx |
| x-1 |
(1)求常数k的值;
(2)设h(x)=
| 1-kx |
| x-1 |
(3)若函数g(x)=f(x)-(
| 1 |
| 2 |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1)由于f(x)为奇函数,可得f(-x)=-f(x),即可得出k;
(2)利用对数函数的单调性和不等式的性质通过作差即可得出;
(3)利用(2)函数f(x)的单调性、指数函数的单调性即可得出.
(2)利用对数函数的单调性和不等式的性质通过作差即可得出;
(3)利用(2)函数f(x)的单调性、指数函数的单调性即可得出.
解答:
解:(1)∵f(x)=log
为奇函数
∴f(-x)=-f(x),
即log
=-log
,
∴1-k2x2=1-x2,整理得k2=1.
∴k=-1(k=1使f(x)无意义而舍去).
(2)∵f(x)=log
=log2
设a>b>1时,
∴f(a)-f(b)=log2
-log2
=log2(
•
)=log2
∵a>b>1时,ab+a-b-1>ab-a+b-1>0,
∴
>1,
从而log2
>0
即f(a)-f(b)>0.
∴f(a)>f(b).
f(x)在(1,+∞)递增
(3)由(2)知,f(x)在(1,+∞)递增,
∴g(x)=f(x)-(
)x+m在[3,4]递增.
∵g(x)在区间[3,4]上没有零点,
∴g(3)=log
-(
)3+m=-
+m>0.
或g(4)=log
-(
)4+m=log
-
+m<0,
∴m>
或m<
-log
| 1 |
| 2 |
| 1-kx |
| x-1 |
∴f(-x)=-f(x),
即log
| 1 |
| 2 |
| 1+kx |
| -x-1 |
| 1 |
| 2 |
| 1-kx |
| x-1 |
∴1-k2x2=1-x2,整理得k2=1.
∴k=-1(k=1使f(x)无意义而舍去).
(2)∵f(x)=log
| 1 |
| 2 |
| 1+x |
| x-1 |
| x-1 |
| x+1 |
设a>b>1时,
∴f(a)-f(b)=log2
| a-1 |
| a+1 |
| b-1 |
| b+1 |
| a-1 |
| a+1 |
| b+1 |
| b-1 |
| ab+a-b-1 |
| ab-a+b-1 |
∵a>b>1时,ab+a-b-1>ab-a+b-1>0,
∴
| ab+a-b-1 |
| ab-a+b-1 |
从而log2
| ab+a-b-1 |
| ab-a+b-1 |
即f(a)-f(b)>0.
∴f(a)>f(b).
f(x)在(1,+∞)递增
(3)由(2)知,f(x)在(1,+∞)递增,
∴g(x)=f(x)-(
| 1 |
| 2 |
∵g(x)在区间[3,4]上没有零点,
∴g(3)=log
| 1 |
| 2 |
| 1+3 |
| 3-1 |
| 1 |
| 2 |
| 9 |
| 8 |
或g(4)=log
| 1 |
| 2 |
| 1+4 |
| 4-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
| 1 |
| 16 |
∴m>
| 9 |
| 8 |
| 1 |
| 16 |
| 1 |
| 2 |
| 5 |
| 3 |
点评:本题考查了函数的奇偶性、单调性、不等式的性质、分类讨论等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
直线x-y=0被圆x2+y2=1截得的弦长为( )
| A、2 | B、1 | C、4 | D、3 |
已知两个变量x,y具有线性相关关系,并测得(x,y)的四组值分别是(2,3)、(5,7)、(8,9)、(11,13),则求得的线性回归方程所确定的直线必定经过点( )
| A、(2,3) |
| B、(8,9) |
| C、(6,9) |
| D、(6.5,8) |
设0<b<1,则log2015b+logb2015的取值范围是( )
| A、[2,+∞) |
| B、(2,+∞) |
| C、(-∞,2] |
| D、(-∞,2) |
为了得到函数y=sin
x的图象,只需把函数y=sinx图象上所有的点的( )
| 1 |
| 3 |
| A、横坐标伸长到原来的3倍,纵坐标不变 | ||
B、横坐标缩小到原来的
| ||
| C、纵坐标伸长到原来的3倍,横坐标不变 | ||
D、纵坐标伸长到原来的
|
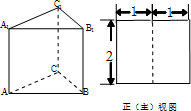 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )