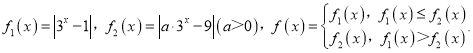题目内容
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)求函数![]() 在
在![]() 的值域;
的值域;
(2)用![]() 表示实数
表示实数![]() ,
,![]() 的最大值,记函数
的最大值,记函数![]() ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)求导得到![]() ,讨论
,讨论![]() 和
和![]() 得到函数
得到函数![]() 在
在![]() 单调递增,计算得到答案.
单调递增,计算得到答案.
(2)![]() 时,
时,![]() 恒成立,当
恒成立,当![]() 时,
时,![]() 恒成立,故
恒成立,故![]() 的零点即为函数
的零点即为函数![]() 的零点,讨论
的零点,讨论![]() 在
在![]() 的零点个数得到答案.
的零点个数得到答案.
(1)![]()
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]()
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]()
所以:当![]() 时,
时,![]() 成立,即函数
成立,即函数![]() 在
在![]() 单调递增
单调递增
所以函数![]() 在
在![]() 的值域为
的值域为![]() ,即值域为
,即值域为![]() .
.
(2)函数![]() 的定义域为
的定义域为![]()
由(1)得,函数![]() 在
在![]() 单调递增,
单调递增,![]()
当![]() 时,
时,![]() ,又
,又![]() ,
,
所以![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 时,
时,![]() 无零点.
无零点.
当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 的零点即为函数
的零点即为函数![]() 的零点
的零点
下面讨论函数![]() 在
在![]() 的零点个数
的零点个数
![]() ,所以
,所以![]()
Ⅰ、当![]() 时,因为
时,因为![]() ,
,![]()
又函数![]() 在区间
在区间![]() 递减,所以
递减,所以![]()
即当![]() 时,
时,![]() ,
,![]()
所以![]() 单调递减,由
单调递减,由![]() 得:当
得:当![]() 时
时![]() ,
,![]() 递增
递增
当![]() 时
时![]() ,
,![]() 递减
递减
当![]() 时
时![]() ,
,![]() ,当
,当![]() 时
时![]()
又![]() ,
,![]()
当![]() 时,函数
时,函数![]() 有1个零点;
有1个零点;
当![]() 时,函数
时,函数![]() 有2个零点;
有2个零点;
当![]() 时,函数
时,函数![]() 有3个零点;
有3个零点;
Ⅱ、当![]() 时,
时,![]() ,由Ⅰ得:当
,由Ⅰ得:当![]() 时,
时,![]() ,
,![]() 递增,
递增,
当![]() 时,
时,![]() ,
,![]() 递减,所以
递减,所以![]() ,
,![]() ,
,
所以当![]() 时函数
时函数![]() 有2个零点
有2个零点
Ⅲ、当![]() 时,
时,![]()
![]() ,
,![]() ,即
,即![]() 成立,由
成立,由![]() ,
,
所以当![]() 时函数
时函数![]() 有1个零点
有1个零点
综上所述:当![]() 或
或![]() 时,函数
时,函数![]() 有1个零点;
有1个零点;
当![]() 或
或![]() 时,函数
时,函数![]() 有2个零点;
有2个零点;
当![]() 时,函数
时,函数![]() 有3个零点.
有3个零点.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目