题目内容
【题目】若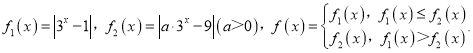
(1)当![]() 时,设
时,设![]() 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为![]() (闭区间
(闭区间![]() 的长度为
的长度为![]() ),试求
),试求![]() 的最大值;
的最大值;
(2)是否存在这样的![]() 使得当
使得当![]() 时,
时,![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() (2)存在,
(2)存在, ![]() 的取值范围为
的取值范围为![]()
【解析】
(1)由具体到一般,针对![]() 的范围条件,作差比较出
的范围条件,作差比较出![]() 与
与![]() 的大小,在
的大小,在![]() 时,自变量
时,自变量![]() 取哪些值时
取哪些值时![]() ,进而确定求出
,进而确定求出![]() 的解析式,对参数的讨论要结合具体的数值,从直观到抽象采取分类策略.
的解析式,对参数的讨论要结合具体的数值,从直观到抽象采取分类策略.
(2)本问利用(1)的结论容易求解,需要注意的是等价转化思想的应用,分类讨论思想重新在本问中的体现.
(1)因为![]() ,所以
,所以![]() ,则
,则
①当![]() 时,
时,
因为![]() ,
,![]() ,
,
所以由![]() ,
,
解得![]() ,
,
从而当![]() 时,
时,![]()
②当![]() 时,
时,
因为![]() ,
,![]() ,
,
所以由![]() ,
,
解得![]() ,
,
从而当![]() 时,
时,![]()
③当![]() 时,
时,
因为![]() ,
,
从而![]() 一定不成立
一定不成立
综上得,当且仅当![]() ,
,![]() 时,
时,![]() ,
,
故![]()
从而当![]() 时,
时,![]() 取得最大值为
取得最大值为![]()
(2)“当![]() ,
,![]() 时,
时,![]() ”等价于“
”等价于“![]() 对
对![]() ,
,![]() 恒成立”,
恒成立”,
即“![]() 对
对![]() ,
,![]() 恒成立”
恒成立”
①当![]() 时,
时,![]() ,
,
则当![]() 时,
时,![]() ,
,
则![]() 可化为
可化为![]() ,即
,即![]() ,
,
而当![]() 时,
时,![]() ,
,
所以![]() ,从而
,从而![]() 适合题意
适合题意
②当![]() 时,
时,![]() .
.
(1)当![]() 时,
时,![]() 可化为
可化为![]() ,即
,即![]() ,而
,而![]() ,
,
所以![]() ,此时要求
,此时要求![]()
(2)当![]() 时,
时,![]() 可化为
可化为![]() ,
,
此时只要求![]()
(3)当![]() 时,
时,![]() 可化为
可化为![]() ,即
,即![]() ,而
,而![]() ,
,
所以![]() ,此时要求
,此时要求![]()
由(1)(2)(3),得![]() 符合题意要求.
符合题意要求.
综合①②知,满足题意的![]() 存在,且
存在,且![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目