题目内容
8.已知三棱锥P-ABC中,△ABC为等边三角形,PA=PB=PC,PA⊥PB,点P到平面ABC的距离为2$\sqrt{3}$,则三棱锥P-ABC的体积为36.分析 设底面边长为a,利用勾股定理计算棱锥的侧棱长,根据勾股定理列方程解出a,再计算棱锥的体积.
解答 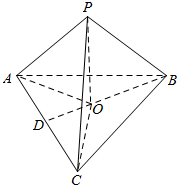 解:设P在底面ABC的投影为O,
解:设P在底面ABC的投影为O,
∵PA=PB=PC,△ABC是等边三角形,
∴O是△ABC的中心,
设△ABC的边长为a,则BD=$\frac{\sqrt{3}}{2}a$,∴OB=$\frac{2}{3}BD$=$\frac{\sqrt{3}}{3}a$.
∴PB=$\sqrt{P{O}^{2}+O{B}^{2}}$=$\sqrt{12+\frac{{a}^{2}}{3}}$.
∵PA⊥PB,∴PA2+PB2=AB2,
即12+$\frac{{a}^{2}}{3}$+12+$\frac{{a}^{2}}{3}$=a2,
解得a=6$\sqrt{2}$.
∴VP-ABC=$\frac{1}{3}{S}_{△ABC}•PO$=$\frac{1}{3}×\frac{\sqrt{3}}{4}{a}^{2}×2\sqrt{3}=\frac{{a}^{2}}{2}$=36.
故答案为:36.
点评 本题考查了正三棱锥的结构特征和体积计算,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
3.集合A={(x,y)|x,y∈R},若x,y∈A,已知x=(x1,y1),y=(x2,y2),定义集合A中元素间的运算x*y,称为“*”运算,此运算满足以下运算规律:
①任意x,y∈A有x*y=y*x
②任意x,y,z∈A有(x+y)*z=x*z+y*z(其中x+y=(x1+x2,y1+y2))
③任意x,y∈A,a∈R有(ax)*y=a(x*y)
④任意x∈A有x*x≥0,且x*x=0成立的充分必要条件是x=(0,0)为向量,如果x=(x1,y1),y=(x2,y2),那么下列运算属于“*”正确运算的是( )
①任意x,y∈A有x*y=y*x
②任意x,y,z∈A有(x+y)*z=x*z+y*z(其中x+y=(x1+x2,y1+y2))
③任意x,y∈A,a∈R有(ax)*y=a(x*y)
④任意x∈A有x*x≥0,且x*x=0成立的充分必要条件是x=(0,0)为向量,如果x=(x1,y1),y=(x2,y2),那么下列运算属于“*”正确运算的是( )
| A. | x*y=x1y1+2x2y2 | B. | x*y=x1y1-x2y2 | C. | x*y=x1y1+x2y2+1 | D. | x*y=2x1x2+y1y2 |
13.已知△ABC的外接圆半径为1,圆心为O,且$\overrightarrow{OA}$$+\overrightarrow{OB}$$+\sqrt{2}$$\overrightarrow{OC}$=0,则△ABC的面积为( )
| A. | 1+$\sqrt{2}$ | B. | $\frac{1}{2}$+$\sqrt{2}$ | C. | 1+$\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}+\frac{\sqrt{2}}{2}$ |