Question

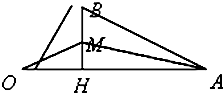如图所示：在△AOB中，∠AOB=

π

3

，OA=3，OB=2，BH⊥OA于H，M为线段BH上的点，且

MO

•

MA

=-

5

4

，若

BM

=x

BO

+y

BA

，则x+y的值等于

 

．

Answer 1

考点：平面向量的基本定理及其意义

专题：平面向量及应用

分析：以HA所在直线为x轴，以HB所在直线为y轴，建立平面直角坐标系，根据已知条件可求得点O，A，B的坐标，设M（0，m），所以可求出向量

MO

，

MA

的坐标，根据

MO

•

MA

=-

5

4

即可求出m的值，所以可求得向量

BM

，

BO

，

BA

的坐标，根据

BM

=x

BO

+y

BA

即可求出x，y，从而求出x+y．

解答： 解：由已知条件知：OH=1，HA=2，BH=

3

；
分别以HA，HB所在直线为x轴，y轴建立如图所示平面直角坐标系，则：O（-1，0），B（0，

3

），A（2，0），设M（0，m）；
∴

MO

=(-1，-m)，

MA

=(2，-m)；
∴

MO

•

MA

=-2+m2=-

5

4

，解得m=

3

2

，∴M(0，

3

2

)；

BM

=(0，-

3

2

)，

BO

=(-1，-

3

)，

BA

=(2，-

3

)；
∴(0，-

3

2

)=x(-1，-

3

)+y(2，-

3

)；
∴

0=-x+2y - 3 2 =- 3 x- 3 y

，解得x=

1

3

，y=

1

6

，
∴x+y=

1

2

．
故答案为：

1

2

．

点评：本题考查建立平面直角坐标系解决问题的方法，数量积的坐标运算，由点的坐标求向量的坐标，向量的坐标相等．