题目内容
4.下列函数中,同时满足条件①f(-x)=-f(x);②若x1<x2有f(x1)<f(x2)的为( )| A. | y=x+1 | B. | y=2cosx | C. | y=-$\frac{1}{x}$ | D. | y=x|x| |
分析 由条件可得f(x)为定义域R上的奇函数,且为增函数,运用常见函数的奇偶性和单调性,即可判断A,B,C错误,D正确.
解答 解:①f(-x)=-f(x),可得f(x)为奇函数;
②若x1<x2有f(x1)<f(x2),可得f(x)为R上的增函数.
对于A,y=x+1为R上的增函数,既不是奇函数,也不是偶函数,故A错误;
对于B,y=2cosx为偶函数,在(2kπ-π,2kπ),k∈Z递增,在(2kπ,2kπ+π),k∈Z递减,故C错误;
对于C,y=-$\frac{1}{x}$为奇函数,且在(-∞,0),(0,+∞)递增,故C错误;
对于D,y=x|x|,有f(-x)=-x|-x|=-x|x|=-f(x),x>0时,y=x2递增,在R上递增,故D正确.
故选:D.
点评 本题考查函数的奇偶性和单调性的判断,考查运算能力和判断能力,属于基础题和易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.投掷一枚均匀骰子,记“骰子向上的点数是偶数”为事件A,“骰子向上的点数6”为事件B,则事件A,B中至少有一件发生的概率是( )
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{2}{3}$ |
19.如图所示,在正方体ABC-A1B1C1D1中,异面直线A1D与AB1所成角( )
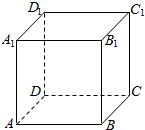

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
9.执行如图所示的程序框图,如果输入的t∈[-1,2],则输出的s属于( )
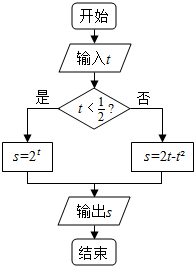

| A. | [0,1] | B. | [$\frac{3}{4}$,$\sqrt{2}$] | C. | [0,$\sqrt{2}$] | D. | [1,$\sqrt{2}$) |
16.执行如图所示的程序框图后,输出的结果为( )
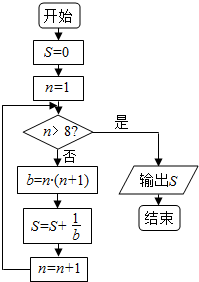

| A. | $\frac{7}{8}$ | B. | $\frac{9}{10}$ | C. | $\frac{8}{9}$ | D. | $\frac{10}{11}$ |