题目内容
如图，在△ABC中，D是边BC上一点，DC=2BD．（1）若
| AB |
| a |
| AC |
| b |
| a |
| b |
| BC |
| AD |
（2）若∠BAC=120°，AB=2，AC=1，求
| BC |
| AD |
（3）若B（-1，
| 3 |
考点：平面向量数量积的运算,平面向量的坐标运算
专题：平面向量及应用
分析：（1）利用向量的三角形法则即可得出；
（2）由∠BAC=120°，AB=2，AC=1，可得
•
=2×1×cos120°=-1．再利用（1）和数量积运算可得
•
=(
-
)•(
+
)=
•
+
2-
2即可得出．．
（3）设D（x，y），利用向量的坐标运算和向量相等即可得出．
（2）由∠BAC=120°，AB=2，AC=1，可得
| a |
| b |
| BC |
| AD |
| b |
| a |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| 1 |
| 3 |
| a |
| b |
| 1 |
| 3 |
| b |
| 2 |
| 3 |
| a |
（3）设D（x，y），利用向量的坐标运算和向量相等即可得出．
解答：
解：（1）∵
=
-
=
-
，
=2
，
∴
=
-
=
+
=
(
-
)+
=
+
．
（2）∵∠BAC=120°，AB=2，AC=1，
∴|
|=2，|
|=1，
•
=2×1×cos120°=-1．
由（1）可得
•
=(
-
)•(
+
)=
•
+
2-
2=
×(-1)+
×12-
×22=-
．
（3）设D（x，y），∵
=2
，B（-1，
），C（1，0），
∴（1-x，-y）=2(x+1，y-
)=(2x+2，2y-2
)，
∴
，解得
，
∴D(-
，
)．
| BC |
| AC |
| AB |
| b |
| a |
| DC |
| BD |
∴
| AD |
| BD |
| BA |
| 1 |
| 3 |
| BC |
| AB |
| 1 |
| 3 |
| b |
| a |
| a |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
（2）∵∠BAC=120°，AB=2，AC=1，
∴|
| a |
| b |
| a |
| b |
由（1）可得
| BC |
| AD |
| b |
| a |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| 1 |
| 3 |
| a |
| b |
| 1 |
| 3 |
| b |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
（3）设D（x，y），∵
| DC |
| BD |
| 3 |
∴（1-x，-y）=2(x+1，y-
| 3 |
| 3 |
∴
|
|
∴D(-
| 1 |
| 3 |
2
| ||
| 3 |
点评：本题考查了向量的三角形法则、数量积运算、向量的坐标运算和向量相等等基础知识，属于中档题．
练习册系列答案
相关题目
正三棱柱ABC-A1B1C1中，BC=2，AA1=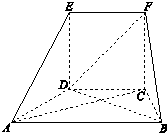
在如图所示的几何体中，面CDEF为正方形，面ABCD为等腰梯形，AB∥CD，AC=