题目内容
下列函数中,是奇函数,又在定义域内为减函数的是( )
A、y=(
| ||
B、y=
| ||
| C、y=-2x3 | ||
| D、y=log2(-x) |
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:计算题,函数的性质及应用
分析:运用定义和常见函数的奇偶性和单调性,即可判断是奇函数,又在定义域内为减函数的函数.
解答:
解:对于A.为指数函数,没有奇偶性,则A错;
对于B.f(-x)=-f(x),则为奇函数,在x<0,x>0上均为减函数,则B错;
对于C.f(-x)=-f(x),则为奇函数,且y′=-6x2≤0,即有减函数,则C对;
对于D.定义域为(-∞,0),不关于原点对称,则不为奇函数,则D错.
故选C.
对于B.f(-x)=-f(x),则为奇函数,在x<0,x>0上均为减函数,则B错;
对于C.f(-x)=-f(x),则为奇函数,且y′=-6x2≤0,即有减函数,则C对;
对于D.定义域为(-∞,0),不关于原点对称,则不为奇函数,则D错.
故选C.
点评:本题考查函数的奇偶性和单调性的判断,注意运用定义和常见函数的奇偶性和单调性,属于基础题和易错题.

练习册系列答案
相关题目
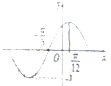 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0),|φ|≤
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0),|φ|≤| π |
| 2 |
A、f(x)=sin(2x+
| ||
B、f(x)=sin(2x-
| ||
C、f(x)=sin(4x+
| ||
D、f(x)=sin(4x-
|
算法程序如图所示,若输入-2,执行该程序后输出的y为( )


| A、3 | B、8 | C、16 | D、0 |
已知等差数列{an}满足a2+a10=4,则a6=( )
| A、-2 | B、2 | C、4 | D、-4 |
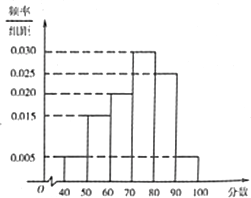 育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为
育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为