题目内容
已知f(x)=-
(x>0).
(1)a1=1,
=-f(an),n∈N*,求{an}的通项;
(2)设Sn=a12+a22+…+an2,bn=S2n+1-Sn,是否存在整数m,对一切n∈N*,都有bn<
成立?若存在,求出m的最小值;若不存在,请说明理由.
|
(1)a1=1,
| 1 |
| an+1 |
(2)设Sn=a12+a22+…+an2,bn=S2n+1-Sn,是否存在整数m,对一切n∈N*,都有bn<
| m |
| 25 |
考点:数列与不等式的综合,数列的应用
专题:计算题,存在型,点列、递归数列与数学归纳法
分析:(1)根据递推数列,利用构造法即可证明数列{
}是首项为1,公差为4的等差数列,由等差数列的通项公式即可得到;
(2)求出{an2}的通项公式,判断{S2n+1-Sn}的单调性,即可求正整数m的最小值.
| 1 |
| an2 |
(2)求出{an2}的通项公式,判断{S2n+1-Sn}的单调性,即可求正整数m的最小值.
解答:
解:(1)a1=1,
=-f(an)=
,
即有
-
=4,
即数列{
}是首项为1,公差为4的等差数列,
则
=1+4(n-1)=4n-3,
故an=
;
(2)由于an2=
,
由于bn=S2n+1-Sn,
则bn-bn+1=(S2n+1-Sn)-(S2n+3-Sn+1)
=(an+12+an+22+…+a2n+12)-(an+22+an+32+…+a2n+32)
=an+12-a2n+22-a2n+32
=
-
-
=(
-
)+(
-
)>0,
∴数列{S2n+1-Sn}(n∈N*)是递减数列,
数列{S2n+1-Sn}(n∈N*)的最大项为
S3-S1=a22+a32=
+
=
,
若
≤
,
∴m≥
,
又∵m是正整数,
∴m的最小值为10.
| 1 |
| an+1 |
|
即有
| 1 |
| an+12 |
| 1 |
| an2 |
即数列{
| 1 |
| an2 |
则
| 1 |
| an2 |
故an=
|
(2)由于an2=
| 1 |
| 4n-3 |
由于bn=S2n+1-Sn,
则bn-bn+1=(S2n+1-Sn)-(S2n+3-Sn+1)
=(an+12+an+22+…+a2n+12)-(an+22+an+32+…+a2n+32)
=an+12-a2n+22-a2n+32
=
| 1 |
| 4n+1 |
| 1 |
| 8n+5 |
| 1 |
| 8n+9 |
| 1 |
| 8n+2 |
| 1 |
| 8n+5 |
| 1 |
| 8n+2 |
| 1 |
| 8n+9 |
∴数列{S2n+1-Sn}(n∈N*)是递减数列,
数列{S2n+1-Sn}(n∈N*)的最大项为
S3-S1=a22+a32=
| 1 |
| 5 |
| 1 |
| 9 |
| 14 |
| 45 |
若
| 14 |
| 45 |
| m |
| 30 |
∴m≥
| 28 |
| 3 |
又∵m是正整数,
∴m的最小值为10.
点评:本题考查数列的通项公式的求法,考查数列前n项和的求法,考查实数的最小值的求法,解题时要认真审题,综合性较强,运算量较大,有一定的难度.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如下:
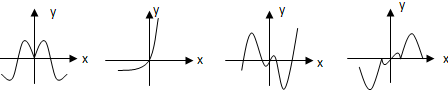
则按照从左到右图象对应的函数序号安排正确的一组是( )

则按照从左到右图象对应的函数序号安排正确的一组是( )
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |
已知f(x)=(4a-3)x+b-2a,x∈[0,1],若f(x)≤2恒成立,则t=a+b的最大值为( )
A、
| ||
| B、4 | ||
C、
| ||
D、
|
 在抛物线y2=16x内有一点G(4,4)抛物线的焦点为F,若以F,G为焦点作一个与抛物线相交且长轴最短的椭圆,则此椭圆的离心率为
在抛物线y2=16x内有一点G(4,4)抛物线的焦点为F,若以F,G为焦点作一个与抛物线相交且长轴最短的椭圆,则此椭圆的离心率为