双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的两个顶点三等分焦距.则双曲线的离心率为( )A．4B．3C．2D．1 题目和参考答案——青夏教育精英家教网—

题目内容

11．双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的两个顶点三等分焦距，则双曲线的离心率为（　　）

A．

B．

C．

D．

分析由题意知，两个顶点三等分焦距，得出a与c的关系，即可计算得解．

解答解：∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的两个顶点三等分焦距，
∴2a=$\frac{1}{3}$2c，c=3a，
∴e=$\frac{c}{a}=3$．
故选：B．

点评本题考查双曲线的几何性质的应用，考查了思想结合思想的应用，属于基础题．

练习册系列答案

相关题目

7．长方体长、宽、高之比为2：3：4，全面积为208，长方体的体积为192．

8．将红、黄、蓝、黑四只铅笔分给三名同学，每名同学至少分到一支铅笔，且红、黄两只铅笔不能分给同一名同学，则不同的分法种数为（　　）

5．已知$\overrightarrow{a}$=（-1，1），$\overrightarrow{a}+\overrightarrow{b}$=（3，4），求向量$\overrightarrow{b}$的坐标．

6．已知函数f（x）=axlnx（a≠0，a∈R）．
（1）若函数f（x）有极小值-$\frac{1}{e}$，求f（x）的单调函数；
（2）证明：当a＞0时，f（x）≥a（x-1）；
（3）当x∈（1，e）是，不等式$\frac{x-1}{a}$＜lnx恒成立，求实数a的取值范围．

16．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{3}+2{x}^{2}-x，0＜x＜1}\\{lnx，x≥1}\end{array}\right.$，对任意t∈（0，+∞），不等式f（t）＜kt恒成立，则实数k的取值范围是$（\frac{1}{e}，+∞）$．

3．在平面直角坐标系xOy中，已知点A（4，3），点B是圆（x+1）²+y²=4上的动点，则线段AB的中点M的轨迹方程是（　　）

A．

${（x-\frac{3}{2}）^2}+{（y-\frac{3}{2}）^2}=1$

B．

${（x-\frac{3}{2}）^2}+{（y-\frac{3}{2}）^2}=4$

20．（x-$\frac{2}{x}$）ⁿ的展开式中只有第5项的二项式系数最大，则它的展开式中常数项是1120．

1．

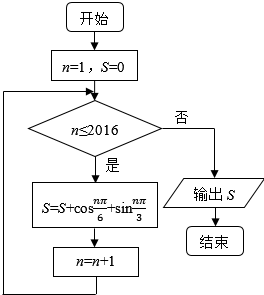执行如图所示的程序框图，则输出结果S=（　　）

$\frac{1-\sqrt{3}}{2}$

D．

$\frac{1+\sqrt{3}}{2}$

试题分类