题目内容
13.在复平面内,复数$\frac{2}{1-i}$-2i2对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的运算法则即可得出.
解答 解:复数$\frac{2}{1-i}$-2i2=$\frac{2(1+i)}{(1-i)(1+i)}$+2=3+i,对应的点(3,1)位于第一象限.
故选:A.
点评 本题考查了复数的运算法则,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
8.已知变量x、t满足约束条件$\left\{\begin{array}{l}{x+2y≥2}\\{2x+y≤4}\\{4x-y≥-1}\end{array}\right.$,则目标函数z=3x-y的最大值是( )
| A. | -4 | B. | -$\frac{3}{2}$ | C. | -1 | D. | 6 |
18.在复平面内,复数$\frac{2}{1-i}$-2对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.长方体ABCD-A1B1C1D1中,AA1=3,AD=4,AB=5,则直线BD1与平面ABCD所成的角的正弦值是( )
| A. | $\frac{4}{5}$ | B. | $\frac{{3\sqrt{2}}}{10}$ | C. | $\frac{3}{{\sqrt{34}}}$ | D. | $\frac{5}{{\sqrt{34}}}$ |
3.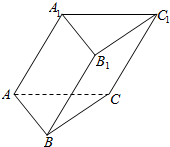 如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )
如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )
 如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )
如图,在三棱柱ABC-A1B1C1中,各棱长均相等,且∠A1AB=∠A1AC=∠BAC=60°,则AB1与底面ABC所成角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
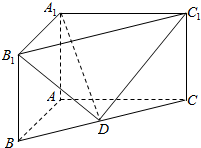 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点,求直线DB1与平面A1C1D所成角的正弦值.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=3,D是BC的中点,求直线DB1与平面A1C1D所成角的正弦值.