题目内容
[已知函数f(x)=loga
是奇函数(a<0且a≠1)
(1)求m的值;
(2)判断f(x)在区间(1,+∞)上的单调性并加以证明;
(3)当a>1,x∈(1,
)时,f(x)的值域是(1,+∞),求a的值.
| 1-mx |
| x-1 |
(1)求m的值;
(2)判断f(x)在区间(1,+∞)上的单调性并加以证明;
(3)当a>1,x∈(1,
| 3 |
考点:对数函数的图像与性质,函数奇偶性的性质
专题:计算题,证明题,函数的性质及应用
分析:(1)由f(x)是奇函数知f(-x)=-f(x)在其定义域内恒成立,从而解出m并检验;
(2)当0<a<1时,函数f(x)在区间(1,+∞)上为增函数,当a>1时,函数f(x)在区间(1,+∞)上为减函数;利用定义证明;
(3)当a>1时,f(x)=loga
在(1,
)上为减函数,要使f(x)在(1,
)上值域是(1,+∞),即loga
>1,可得
>a.从而构造函数求解.
(2)当0<a<1时,函数f(x)在区间(1,+∞)上为增函数,当a>1时,函数f(x)在区间(1,+∞)上为减函数;利用定义证明;
(3)当a>1时,f(x)=loga
| x+1 |
| x-1 |
| 3 |
| 3 |
| x+1 |
| x-1 |
| x+1 |
| x-1 |
解答:
解:(1)∵f(x)是奇函数,
∴f(-x)=-f(x)在其定义域内恒成立,
即loga
=-loga
,
∴1-m2x2=1-x2,
∴m=-1或m=1(舍去),
∴m=-1.
(2)当0<a<1时,函数f(x)在区间(1,+∞)上为增函数,
当a>1时,函数f(x)在区间(1,+∞)上为减函数,证明如下,
由(1)得f(x)=loga
(a>0且a≠1),
设t(x)=
,任取x1,x2∈(1,+∞),且x1<x2
∴t(x1)-t(x2)=
-
=
,
∵x1>1,x2>1,x1<x2
∴t(x1)>t(x2),
即
>
;
所以当a>1时,loga
>loga
即f(x1)>f(x2)
函数f(x)在区间(1,+∞)上为减函数;
所以当0<a<1时,loga
<loga
即f(x1)<f(x2)
函数f(x)在区间(1,+∞)上为增函数;
(3)当a>1时,f(x)=loga
在(1,
)上为减函数,
要使f(x)在(1,
)上值域是(1,+∞),即loga
>1,可得
>a.
令g(x)=
=1+
在(1,
)上是减函数.
所以g(x)∈(1+
,+∞),
所以a=1+
=2+
.所以a=2+
.
∴f(-x)=-f(x)在其定义域内恒成立,
即loga
| 1+mx |
| -x-1 |
| 1-mx |
| x-1 |
∴1-m2x2=1-x2,
∴m=-1或m=1(舍去),
∴m=-1.
(2)当0<a<1时,函数f(x)在区间(1,+∞)上为增函数,
当a>1时,函数f(x)在区间(1,+∞)上为减函数,证明如下,
由(1)得f(x)=loga
| x+1 |
| x-1 |
设t(x)=
| x+1 |
| x-1 |
∴t(x1)-t(x2)=
| x1+1 |
| x1-1 |
| x2+1 |
| x2-1 |
| 2(x2-x1) |
| (x1-1)(x2-1) |
∵x1>1,x2>1,x1<x2
∴t(x1)>t(x2),
即
| x1+1 |
| x1-1 |
| x2+1 |
| x2-1 |
所以当a>1时,loga
| x1+1 |
| x1-1 |
| x2+1 |
| x2-1 |
函数f(x)在区间(1,+∞)上为减函数;
所以当0<a<1时,loga
| x1+1 |
| x1-1 |
| x2+1 |
| x2-1 |
函数f(x)在区间(1,+∞)上为增函数;
(3)当a>1时,f(x)=loga
| x+1 |
| x-1 |
| 3 |
要使f(x)在(1,
| 3 |
| x+1 |
| x-1 |
| x+1 |
| x-1 |
令g(x)=
| x+1 |
| x-1 |
| 2 |
| x-1 |
| 3 |
所以g(x)∈(1+
| 2 | ||
|
所以a=1+
| 2 | ||
|
| 3 |
| 3 |
点评:本题考查了函数的性质的判断与应用,属于中档题.

练习册系列答案
相关题目
已知圆O:x2+y2=1,直线l:3x+4y-3=0,则直线l被圆O所截的弦长为( )
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
直线y=
x的倾斜角为( )
| ||
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
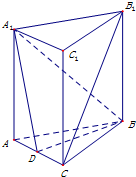 如图,在直三棱柱ABC-A1B1C1中,cos∠A1DD1=
如图,在直三棱柱ABC-A1B1C1中,cos∠A1DD1=
 向高为H的圆锥形漏斗注入化学溶液(漏斗下方口暂时关闭),注入溶液量V与溶液深度h的函数图象是( )
向高为H的圆锥形漏斗注入化学溶液(漏斗下方口暂时关闭),注入溶液量V与溶液深度h的函数图象是( )


