题目内容
8.已知数列{an}满足a1=-2,an+1=2an+4.( I)求证{an+4}是等比数列,并求数列{an}的通项公式;
( II)求数列{an}的前n项的和Sn.
分析 (Ⅰ)an+1=2an+4,变形为an+1+4=2(an+4),利用等比数列的通项公式即可得出.
( II)由(Ⅰ)可知,${a_n}={2^n}-4$,利用等比数列的求和公式即可得出.
解答 解:(Ⅰ)证明:an+1=2an+4,变形为an+1+4=2(an+4).--------------(2分)
又∵a1=-2,∴a1+4=2∴数列{an+4}为以2为首项,2为公比的等比数列--------------(4分)∴${a_n}+4={2^n},{a_n}={2^n}-4$-------------(6分)
( II)由(Ⅰ)可知,${a_n}={2^n}-4$
∴Sn=2+22+…+2n-4n,------------------------(9分)
=$\frac{{2({1-{2^n}})}}{1-2}-4n={2^{n+1}}-4n-2$------------------------(12分)
点评 本题考查了等比数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
19.设i为虚数单位,则复数$z=\frac{1-i}{1+i}$的模为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
3.把函数f(x)=$\sqrt{3}$cos2x-sin2x的图象向右平移$\frac{π}{12}$个单位得到函数y=g(x)的图象,则函数y=g(x)在下列哪个区间是单调递减的( )
| A. | [-$\frac{π}{2}$,0] | B. | [-π,0] | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [0,$\frac{π}{2}$] |
13.已知复数z=|1-i|i2017(其中i为虚数单位),则$\overline z$的虚部为( )
| A. | -1 | B. | -i | C. | $\sqrt{2}i$ | D. | $-\sqrt{2}$ |
20.为了解人们对城市治安状况的满意度,某部门对城市部分居民的“安全感”进行调查,在调查过程中让每个居民客观地对自己目前生活城市的安全感进行评分,并把所得分作为“安全感指数”,即用区间[0,100]内的一个数来表示,该数越接近100表示安全感越高.现随机对该地区的男、女居民各500人进行了调查,调查数据如表所示:
根据表格,解答下面的问题:
(Ⅰ)估算该地区居民安全感指数的平均值;
(Ⅱ)如果居民安全感指数不小于60,则认为其安全感好.为了进一步了解居民的安全感,调查组又在该地区随机抽取3对夫妻进行调查,用X表示他们之中安全感好的夫妻(夫妻二人都感到安全)的对数,求X的分布列及期望(以样本的频率作为总体的概率).
| 安全感指数 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100] |
| 男居民人数 | 8 | 16 | 226 | 131 | 119 |
| 女居民人数 | 12 | 14 | 174 | 122 | 178 |
(Ⅰ)估算该地区居民安全感指数的平均值;
(Ⅱ)如果居民安全感指数不小于60,则认为其安全感好.为了进一步了解居民的安全感,调查组又在该地区随机抽取3对夫妻进行调查,用X表示他们之中安全感好的夫妻(夫妻二人都感到安全)的对数,求X的分布列及期望(以样本的频率作为总体的概率).
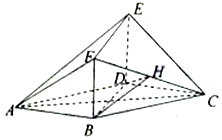 如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.
如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.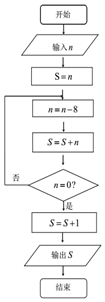 《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.
《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.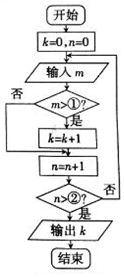 现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )
现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )