题目内容
如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点.
(1)若PN=NC,求证:MN∥平面PAD;
(2)试写出(1)的逆命题,并判断其真假.若为真,请证明;若为假,请举反例.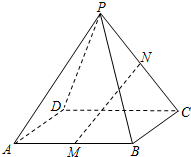
(1)若PN=NC,求证:MN∥平面PAD;
(2)试写出(1)的逆命题,并判断其真假.若为真,请证明;若为假,请举反例.

(1)取CD的中点E,连接ME,NE,
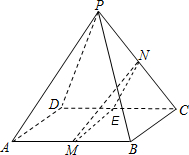
则NE∥PD,ME∥AD
又∵NE?平面MNE,ME?平面MNE,ME∩NE=E
AD?平面APD,PD?平面APD,PD∩AD=D
故平面MNE∥平面PAD
又∵MN?平面MNE,
∴MN∥平面PAD
(2)(1)的逆命题为:若MN∥平面PAD,则PN=NC,这也是一个真命题,理由如下:
取CD的中点E,连接ME,NE,

则NE∥PD,则NE∥平面ADP
又由MN∥平面PAD
MN∩ME=M
则平面MNE∥平面PAD
由面面平行的性质得,ME∥PD
∵E为DC的中点,故N这PC的中点,
故PN=NC

则NE∥PD,ME∥AD
又∵NE?平面MNE,ME?平面MNE,ME∩NE=E
AD?平面APD,PD?平面APD,PD∩AD=D
故平面MNE∥平面PAD
又∵MN?平面MNE,
∴MN∥平面PAD
(2)(1)的逆命题为:若MN∥平面PAD,则PN=NC,这也是一个真命题,理由如下:
取CD的中点E,连接ME,NE,

则NE∥PD,则NE∥平面ADP
又由MN∥平面PAD
MN∩ME=M
则平面MNE∥平面PAD
由面面平行的性质得,ME∥PD
∵E为DC的中点,故N这PC的中点,
故PN=NC

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
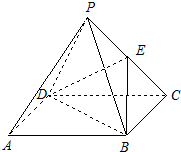 如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.
如图,在正四棱锥P-ABCD中,PA=AB=a,点E在棱PC上.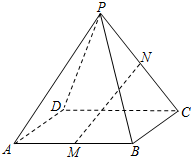 17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点.
17、如图,在正四棱锥P-ABCD中,点M为棱AB的中点,点N为棱PC上的点. 如图,在正四棱锥P-ABCD中,若
如图,在正四棱锥P-ABCD中,若 (2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知
(2013•宿迁一模)如图,在正四棱锥P-ABCD中,已知 如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )
如图,在正四棱锥P-ABCD中,∠APC=60°,则二面角A-PB-C的平面角的余弦值为( )