题目内容
若a，b，c依次表示方程2x+x=1，log2x+x=1，log2x+x=2的根，则a，b，c的大小顺序为（ ）
| A、c＜a＜b |
| B、a＜b＜c |
| C、a＜c＜b |
| D、c＜b＜a |
考点：函数的零点
专题：
分析：转化为：f（x）=2x，与y=1-x交点，h（x）=log2x，与y=1-x交点，h（x）=log2x，与y=2-x交点，图象判断即可．
解答：
解：∵2x+x=1，log2x+x=1，log2x+x=2的根
∴转化为：f（x）=2x，与y=1-x交点
h（x）=log2x，与y=1-x交点
h（x）=log2x，与y=2-x交点，
运用图象判断即可．a=0，b=1，c＞1
故选：B
解：∵2x+x=1，log2x+x=1，log2x+x=2的根∴转化为：f（x）=2x，与y=1-x交点
h（x）=log2x，与y=1-x交点
h（x）=log2x，与y=2-x交点，
运用图象判断即可．a=0，b=1，c＞1
故选：B
点评：本小题主要考查函数单调性的应用、函数的零点、函数的零点与方程根的关系、不等式的解法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
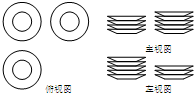一张桌子上摆放有若干个大小、形状完全相同的碟子，现从三个方向看，三种视图如下所示，则这张桌子上碟子的个数为（ ）| A、11 | B、12 | C、13 | D、14 |
已知
、
是平面向量，若
⊥(
-2
)，
⊥(
-2
)，则
与
的夹角是（ ）
| a |
| b |
| a |
| a |
| b |
| b |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
，
满足
⊥
，|
|=2，|
|=1，则|
-2
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、0 | ||
| B、4 | ||
| C、8 | ||
D、2
|