题目内容
已知空间一点A的坐标是（5，2，-6），P点在x轴上，若PA=7，则P点的坐标是 ．
考点：空间中的点的坐标
专题：空间位置关系与距离
分析：设出P的坐标，利用PA=5，求解即可．
解答：
解：设P的坐标是（a，0，0），点A的坐标为（5，2，-6），PA=7，
∴
=7
解得a=8或2
∴P点的坐标是：（8，0，0）或（2，0，0）
故答案为：（8，0，0）或（2，0，0）
∴
| (a-5)2+4+36 |
解得a=8或2
∴P点的坐标是：（8，0，0）或（2，0，0）
故答案为：（8，0，0）或（2，0，0）
点评：本题考查空间两点间的距离公式的应用，考查计算能力．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
出租车按如下方法收费：起步价7元，可行3km（不含3km）；3km到7km（不含7km）按1.6元/km计价（不足1km按1km计算）；7km以后按2.2元/km计价，到目的地结算时还需付1元的燃油附加费．若从甲地坐出租车到乙地（路程12.2km），需付车费（精确到1元）（ ）
| A、28元 | B、27元 |
| C、26元 | D、25元 |
某几何体的三视图如图所示，根据图中标出的数据，可得这个几何体的体积为（ ）
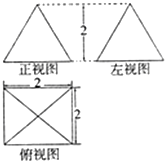
A、4+4
| ||
B、4+4
| ||
C、
| ||
| D、12 |
设α是空间中的一个平面，l，m，n是三条不同的直线，则下列命题中正确的是（ ）
| A、若m?α，n?α，l⊥m，l⊥n，则l⊥α |
| B、若m?α，n⊥α，l⊥n，则l∥m |
| C、若l⊥m，l⊥n，则n∥m |
| D、若m⊥α，n⊥α，则n∥m |
已知点P，A，B在双曲线
-
=1上，直线AB过坐标原点，且直线PA、PB的斜率之积为
，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|