题目内容
对于集合M,定义函数fM(x)=
对于两个集合M,N,定义集合M△N={x|fM(x)•fN(x)=-1}.已知A={2,4,6,8,10},B={1,2,4,8,16}.
(1)用列举法写出集合A△B= ;
(2)用Card(M)表示有限集合M所含元素的个数,当Card(X△A)+Card(X△B)取最小值时集合X的可能情况有 种.
|
(1)用列举法写出集合A△B=
(2)用Card(M)表示有限集合M所含元素的个数,当Card(X△A)+Card(X△B)取最小值时集合X的可能情况有
考点:集合中元素个数的最值,集合的表示法
专题:新定义,集合
分析:(1)利用新集合的定义,研究集合A△B的元素特征,得出A△B集合;(2)利用新集合A△B的定义,理解集合Card(X△A)和集合Card(X△B)中的元素个数概念,根据个数和最小的情况,研究出集合X的元素特征,得到集合X与A∪B,A∩B的关系,从而求出集合X的可能情况.
解答:
解:(1)∵函数fM(x)=
,
∴fM(x)和fN(x)的可能值为1或-1.
根据集合M△N地定义,有fM(x)•fN(x)=-1,
∴fM(x)=1,fN(x)=-1或者fM(x)=-1,fN(x)=1.
即
或者
.
记集合A△B的元素为x,
则有:
或者
.
∵A={2,4,6,8,10},B={1,2,4,8,16}.
∴x可取1,6,10,16.
∴集合A△B={1,6,10,16}.
(2)∵集合A△B的元素为x,则有:
或者
,
∴x∈A∪B,x∉A∩B.
要使Card(X△A)最小,必须Card(X∪A)最小,同时Card(X∩A)最大,
要使Card(X△A)+Card(X△B)取最小,则A∩B⊆X⊆A∪B.
例如:当X=A∩B={2,4,8}时,X△A={6,10},X△B={1,16},Card(X△A)=2,Card(X△B)=2,Card(X△A)+Card(X△B)=4;
当X={2,4,8,6}时,X△A={10},X△B={1,6,16},Card(X△A)=1,Card(X△B)=3,Card(X△A)+Card(X△B)=4;
当X={2,4,8,6,16}时,X△A={10,16},X△B={1,6},Card(X△A)=2,Card(X△B)=2,Card(X△A)+Card(X△B)=4;
…
∴2∉X,4∉X,8∉X恒成立,
1∉X,6∈X,10∈X,16∉X,有可能成立.
即A∪B⊆X⊆A∩B.
∵Card(A∪B)=8,Card(A∩B)=4,
∴Card(A∪B)-Card(A∩B)=4.
集合X是{2,4,8}和{1,6,10,16}的子集的并集.
∵{1,6,10,16}的子集个数为 24=16,
∴集合X的可能情况有16种.
故答案为:(1){1,6,10,16};(2)16.
|
∴fM(x)和fN(x)的可能值为1或-1.
根据集合M△N地定义,有fM(x)•fN(x)=-1,
∴fM(x)=1,fN(x)=-1或者fM(x)=-1,fN(x)=1.
即
|
|
记集合A△B的元素为x,
则有:
|
|
∵A={2,4,6,8,10},B={1,2,4,8,16}.
∴x可取1,6,10,16.
∴集合A△B={1,6,10,16}.
(2)∵集合A△B的元素为x,则有:
|
|
∴x∈A∪B,x∉A∩B.
要使Card(X△A)最小,必须Card(X∪A)最小,同时Card(X∩A)最大,
要使Card(X△A)+Card(X△B)取最小,则A∩B⊆X⊆A∪B.
例如:当X=A∩B={2,4,8}时,X△A={6,10},X△B={1,16},Card(X△A)=2,Card(X△B)=2,Card(X△A)+Card(X△B)=4;
当X={2,4,8,6}时,X△A={10},X△B={1,6,16},Card(X△A)=1,Card(X△B)=3,Card(X△A)+Card(X△B)=4;
当X={2,4,8,6,16}时,X△A={10,16},X△B={1,6},Card(X△A)=2,Card(X△B)=2,Card(X△A)+Card(X△B)=4;
…
∴2∉X,4∉X,8∉X恒成立,
1∉X,6∈X,10∈X,16∉X,有可能成立.
即A∪B⊆X⊆A∩B.
∵Card(A∪B)=8,Card(A∩B)=4,
∴Card(A∪B)-Card(A∩B)=4.
集合X是{2,4,8}和{1,6,10,16}的子集的并集.
∵{1,6,10,16}的子集个数为 24=16,
∴集合X的可能情况有16种.
故答案为:(1){1,6,10,16};(2)16.
点评:本题考查了元素与集合的关系、集合与集合的关系、子集个数等知识点,还考查了学生对新定义概念的理解和应用,思维能力要求高,属于难题.

练习册系列答案
相关题目
对于R上可导的任意函数f(x),若满足(2-x)f′(x)≤0,则必有( )
| A、f(1)+f(3)<2f(2) |
| B、f(1)+f(3)≤2f(2) |
| C、f(1)+f(3)>2f(2) |
| D、f(1)+f(3)≥2f(2) |
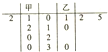 2014年1月8日是传统的腊八节,大家开始购买年货,某淘宝网店趁势推出“抢红包”的促销活动,已知每人有5次抢红包的机会,每次可得1至30元不等的红包,甲、乙二人在这5次抢红包活动中获得红包金额的茎叶图如图所示,若甲5次获得红包金额的均值为
2014年1月8日是传统的腊八节,大家开始购买年货,某淘宝网店趁势推出“抢红包”的促销活动,已知每人有5次抢红包的机会,每次可得1至30元不等的红包,甲、乙二人在这5次抢红包活动中获得红包金额的茎叶图如图所示,若甲5次获得红包金额的均值为