题目内容
3.将函数y=sinx-$\sqrt{3}$cosx的图象沿x轴向右平移a个单位(a>0),所得图象关于y轴对称,则a的值可以是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{2}$ | C. | -$\frac{π}{6}$ | D. | $\frac{π}{3}$ |
分析 根据函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,得出结论.
解答 解:将函数y=sinx-$\sqrt{3}$cosx=2sin(x-$\frac{π}{3}$)的图象沿x轴向右平移a个单位(a>0),可得y=2sin[(x-a)-$\frac{π}{3}$]=2sin(x-a-$\frac{π}{3}$)的图象,
根据所得图象关于y轴对称,可得a+$\frac{π}{3}$=kπ+$\frac{π}{2}$,即a=kπ+$\frac{π}{6}$,k∈Z,
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
14.已知函数f(x)在定义域[2-a,3]上是偶函数,在[0,3]上单调递增,并且f(-m2-$\frac{a}{5}$)>f(-m2+2m-2),则m的取值范围是( )
| A. | $(1-\sqrt{2},\sqrt{2}]$ | B. | $[1-\sqrt{2},\sqrt{2}]$ | C. | $[\frac{1}{2},\sqrt{2}]$ | D. | $(\frac{1}{2},\sqrt{2}]$ |
8.已知x>0,y>0,x+y+$\sqrt{xy}$=2,则x+y的最小值是( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
12.等比数列{an}中,a2=9,a5=243,则a1与a7的等比中项为( )
| A. | ±81 | B. | 81 | C. | -81 | D. | 27 |
 定理:平面内的一条直线与平面的一条斜线在平面内的射影垂直,则这条线段垂直于斜线.
定理:平面内的一条直线与平面的一条斜线在平面内的射影垂直,则这条线段垂直于斜线.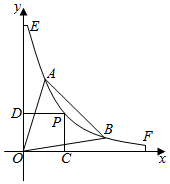 家用电脑桌的桌面采用直线与弧线相结合,前部采用弧线,后部改用直线型.现将电脑桌靠在墙边,沿墙面建立如图所示的直角坐标系.弧线EF的方程为y=$\frac{60}{x}$(5≤x≤12).键盘抽屉所在直线x+y-16=0与弧线交于A,B两点.拟在弧线EF上选取一点P分别作x轴、y轴的垂线.垂足为C,D.四边形OCPD(O为坐标原点)与三角形OAB的公共区域内放置电脑.设点P的坐标为(x,y).公共部分面积为S.(单位:分米)
家用电脑桌的桌面采用直线与弧线相结合,前部采用弧线,后部改用直线型.现将电脑桌靠在墙边,沿墙面建立如图所示的直角坐标系.弧线EF的方程为y=$\frac{60}{x}$(5≤x≤12).键盘抽屉所在直线x+y-16=0与弧线交于A,B两点.拟在弧线EF上选取一点P分别作x轴、y轴的垂线.垂足为C,D.四边形OCPD(O为坐标原点)与三角形OAB的公共区域内放置电脑.设点P的坐标为(x,y).公共部分面积为S.(单位:分米)