题目内容
求下列函数的定义域
（1）y=（x-2）
（2）y=log2（9-x2）
（3）y=
．
（1）y=（x-2）
| 1 |
| 4 |
（2）y=log2（9-x2）
（3）y=
| 1 |
| x-1 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件即可求函数的定义域．
解答：
解：（1）要使函数y=（x-2）
有意义，则x-2≥0，即x≥2，故函数的定义域为[2，+∞）．
（2）要使函数有意义，则9-x2＞0，解得-3＜x＜3，故函数的定义域为（-3，3）．
（3）要使函数有意义，则x-1≠0，即x≠1，故函数的定义域为{x|x≠1}．
| 1 |
| 4 |
（2）要使函数有意义，则9-x2＞0，解得-3＜x＜3，故函数的定义域为（-3，3）．
（3）要使函数有意义，则x-1≠0，即x≠1，故函数的定义域为{x|x≠1}．
点评：本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．
练习册系列答案
相关题目
角733°是（ ）
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
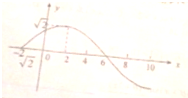已知函数f（x）=Asin（ωt+φ）（A＞0，ω＞0，|φ|＜