题目内容
4.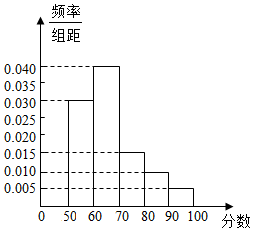 某校举行的数学知识竞赛中,将参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.
某校举行的数学知识竞赛中,将参赛学生的成绩在进行整理后分成5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.(1)求成绩在50-70分的频率是多少;
(2)求这次参赛学生的总人数是多少;
(3)求这次数学竞赛成绩的平均分的近似值.
分析 (1)根据频率分布直方图计算成绩在50-70分的频率值;
(2)根据频数、频率与样本容量的关系求出这次参赛学生的总人数;
(3)利用频率分布直方图估计这次数据的平均值.
解答 解:(1)成绩在50-70分的频率为(0.030+0.040)×10=0.7;
(2)∵第三小组的频数是15,频率为0.015×10=0.15,
∴这次参赛学生的总人数是$\frac{15}{0.15}$=100;
(3)利用频率分布直方图估计这次数学竞赛成绩的平均分是
55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67.
点评 本题考查了利用频率分布直方图求数据的频率、频数、样本容量以及平均数的应用问题,是基础题目.

练习册系列答案
相关题目
15.若0<x<π,则x与sinx的大小关系( )
| A. | x<sinx | B. | x>sinx | C. | x=sinx | D. | 与x的取值有关 |
19.设集合$A=\{x|-\sqrt{2}≤x≤\sqrt{2}\}$,B={整数集},则A∩B=( )
| A. | {-2,-1,0,1,2} | B. | {-1,0,1} | C. | {-2,-1,1,2} | D. | {-1,1} |
14.已知集合A={(x,y)|$\left\{\begin{array}{l}{x+y=1}\\{2-y=2}\end{array}\right.$,x∈R,y∈R},则与A相等的集合是( )
| A. | (1,0) | B. | x=1,y=0 | C. | {(1,0)} | D. | {0,1} |