题目内容
已知离心率为e的椭圆
+
=1(a>b>0)与双曲线x2-y2=1有相同的焦点,且直线y=ex分别与椭圆相交于A、B两点,与双曲线相交于C、D两点,若C、O(坐标原点)、D依次为线段AB的四等分点,则e= .
| x2 |
| a2 |
| y2 |
| b2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:由题意,求出椭圆半焦距c=
,得出a2与b2的关系以及离心率e的表示,由直线y=ex与双曲线方程联立,求出交点坐标,
再由中点坐标公式得出直线与椭圆的交点坐标,代入椭圆方程,求出a的值,即得椭圆的离心率e.
| 2 |
再由中点坐标公式得出直线与椭圆的交点坐标,代入椭圆方程,求出a的值,即得椭圆的离心率e.
解答:
解:∵椭圆
+
=1(a>b>0)与双曲线x2-y2=1有相同的焦点,
∴c=
,
∴a2-b2=2;
∴e=
=
;
又直线y=ex与双曲线相交于C、D两点,
∴
,
即x2-e2x2=1,
解得x=±
=±
;
取x=
,
则y=ex=
•
=
,
∴点B(2x,2y)在椭圆上,
即
+
=1(*);
设t=
>0,
则方程(*)化为4t+8t2=1,
解得t=
,
∴a2-2=
=2
+2,
∴a2=2
+4=(
+1)2,
解得a=
+1;
∴离心率为e=
=
=
.
故答案为:
.
| x2 |
| a2 |
| y2 |
| b2 |
∴c=
| 2 |
∴a2-b2=2;
∴e=
| c |
| a |
| ||
| a |
又直线y=ex与双曲线相交于C、D两点,
∴
|
即x2-e2x2=1,
解得x=±
|
| a | ||
|
取x=
| a | ||
|
则y=ex=
| ||
| a |
| a | ||
|
| ||
|
∴点B(2x,2y)在椭圆上,
即
| 4a2 |
| a2(a2-2) |
| 8 |
| (a2-2)(a2-2) |
设t=
| 1 |
| a2-2 |
则方程(*)化为4t+8t2=1,
解得t=
| ||
| 4 |
∴a2-2=
| 4 | ||
|
| 3 |
∴a2=2
| 3 |
| 3 |
解得a=
| 3 |
∴离心率为e=
| c |
| a |
| ||
|
| ||||
| 2 |
故答案为:
| ||||
| 2 |
点评:本题考查了椭圆的标准方程与几何性质的应用问题,也考查了直线与圆锥曲线的应用问题,是综合题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
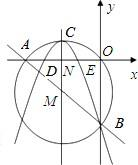 如图所示,在平面直角坐标系中,圆M经过原点O且与x轴y轴分别相交于A(-6,0),B(0,-8)两点,若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过B.
如图所示,在平面直角坐标系中,圆M经过原点O且与x轴y轴分别相交于A(-6,0),B(0,-8)两点,若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过B. 如图,三棱锥P-ABC,底面ABC为边长为2
如图,三棱锥P-ABC,底面ABC为边长为2