题目内容
15．已知定义在R上的偶函数f（x）在[0，+∞）单调递增，若f（lnx）＜f（2），则x的取值范围是（ ）| A． | （0，e2） | B． | （e-2，+∞） | C． | （e2，+∞） | D． | （e-2，e2） |
分析 根据题意，由函数的奇偶性与单调性分析可得f（lnx）＜f（2）?|lnx|＜2，解|lnx|＜2可得x的取值范围，即可得答案．
解答 解：根据题意，f（x）为偶函数且在[0，+∞）单调递增，
则f（lnx）＜f（2）?|lnx|＜2，
即-2＜lnx＜2，
解可得：e-2＜x＜e2
即x的取值范围是（e-2，e2）
故选：D．
点评 本题考查函数奇偶性与单调性的综合应用，涉及对数不等式的解法，关键是分析得到|lnx|＜2．
练习册系列答案
相关题目
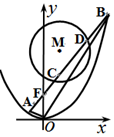已知抛物线G的顶点在原点，焦点在y轴正半轴上，抛物线上的点P（m，4）到其焦点F的距离等于5．
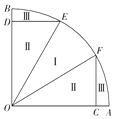现有一个以OA、OB为半径的扇形池塘，在OA、OB上分别取点C、D，作DE∥OA、CF∥OB分别交弧AB于点E、F，且BD=AC，现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的养殖区域．已知OA=1km，∠AOB=$\frac{π}{2}$，∠EOF=θ（0＜θ＜$\frac{π}{2}$）．
20．已知函数f（x）=$\left\{\begin{array}{l}lnx，x＞1\\ \frac{1}{4}x+1，x≤1\end{array}$，g（x）=ax，则方程g（x）=f（x）恰有两个不同的实根时，实数a的取值范围是（ ）（注：e为自然对数的底数）
| A． | $（{0，\frac{1}{e}}）$ | B． | $[{\frac{1}{4}，\frac{1}{e}}）$ | C． | $（{0，\frac{1}{4}}]$ | D． | $（{\frac{1}{4}，e}）$ |