题目内容
13.P(3,y)为α终边上一点,$cosα=\frac{3}{5}$,则y=( )| A. | -3 | B. | 4 | C. | ±3 | D. | ±4 |
分析 利用余弦函数的定义,即可得出结论.
解答 解:∵P(3,y)为α终边上一点,$cosα=\frac{3}{5}$,
∴$\frac{3}{\sqrt{9+{y}^{2}}}$=$\frac{3}{5}$,
∴y=±4,
故选D.
点评 本题主要考查任意角的三角函数的定义,属于基础题.

练习册系列答案
相关题目
3.圆锥过轴的截面是( )
| A. | 圆 | B. | 等腰三角形 | C. | 矩形 | D. | 抛物线 |
1.已知函数f(x)=loga(6-ax)在(-3,2)上是减函数,则a的取值范围是( )
| A. | (0,3) | B. | (1,3] | C. | (1,3) | D. | [3,+∞) |
18.已知椭圆C1和抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于表中:
(1)求椭圆C1和抛物线C2的标准方程;
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,点P(4,0),设$\overrightarrow{FA}=λ\overrightarrow{FB},λ∈[{-2,-1}]$,求$|{\overrightarrow{PA}+\overrightarrow{PB}}|$取最大值时,直线l的斜率.
| x | $-\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | $-\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,点P(4,0),设$\overrightarrow{FA}=λ\overrightarrow{FB},λ∈[{-2,-1}]$,求$|{\overrightarrow{PA}+\overrightarrow{PB}}|$取最大值时,直线l的斜率.
5.已知圆(x+a)2+y2=4截直线x-y-4=0所得的弦的长度为$2\sqrt{2}$,则a等于( )
| A. | $±2\sqrt{2}$ | B. | 6 | C. | 2或6 | D. | -2或-6 |
2.曲线的参数方程为$\left\{\begin{array}{l}x=1+2cosθ\\ y=2+3sinθ\end{array}\right.(θ为参数)$,则该曲线的普通方程为( )
| A. | $\frac{{{{(x+1)}^2}}}{4}-\frac{{{{(y+2)}^2}}}{9}=1$ | B. | $\frac{{{{(x-1)}^2}}}{4}-\frac{{{{(y-2)}^2}}}{9}=1$ | C. | $\frac{{{{(x+1)}^2}}}{4}+\frac{{{{(y+2)}^2}}}{9}=1$ | D. | $\frac{{{{(x-1)}^2}}}{4}+\frac{{{{(y-2)}^2}}}{9}=1$ |
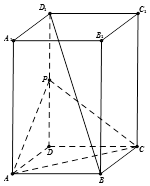 .如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
.如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.