题目内容
11.设x∈R,向量$\overrightarrow a=({x,1}),\overrightarrow b=({4,-2})$,且$\overrightarrow a∥\overrightarrow b$,则$|{\overrightarrow a+\overrightarrow b}|$=( )| A. | $\sqrt{5}$ | B. | 5 | C. | $\sqrt{85}$ | D. | 85 |
分析 根据向量平行求出x的值,在计算模长$|{\overrightarrow a+\overrightarrow b}|$.
解答 解:向量$\overrightarrow a=({x,1}),\overrightarrow b=({4,-2})$,且$\overrightarrow a∥\overrightarrow b$,
∴4×1-(-2)•x=0,
解得x=-2,
∴$\overrightarrow{a}$=(-2,1);
∴$\overrightarrow{a}$+$\overrightarrow{b}$=(2,-1),
∴$|{\overrightarrow a+\overrightarrow b}|$=$\sqrt{{{2}^{2}+(-1)}^{2}}$=$\sqrt{5}$.
故选:A.
点评 本题考查了平面向量的共线定理与模长公式的应用问题,是基础题.

练习册系列答案
相关题目
16.设a,b,c>0,则$a+\frac{1}{b},b+\frac{1}{c},c+\frac{1}{a}$( )
| A. | 都不大于2 | B. | 都不小于2 | ||
| C. | 至少有一个不大于2 | D. | 至少有一个不小于2 |
3.某几何体的三视图中的三角形都是直角三角形.如图所示.则该几何体中直角三角形的个数为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.在棱长为2的正方体ABCD-A1B1C1D1中,M是棱A1D1的中点,过C1,B,M作正方体的截面,则这个截面的面积为( )
| A. | $\frac{3\sqrt{5}}{2}$ | B. | $\frac{3\sqrt{5}}{8}$ | C. | $\frac{9}{2}$ | D. | $\frac{9}{8}$ |

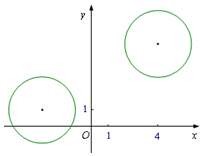 在平面直角坐标系xOy中,已知圆${C_1}:{(x+3)^2}+{(y-1)^2}=4$和圆${C_2}:{(x-4)^2}+{(y-5)^2}=4$.
在平面直角坐标系xOy中,已知圆${C_1}:{(x+3)^2}+{(y-1)^2}=4$和圆${C_2}:{(x-4)^2}+{(y-5)^2}=4$.