题目内容
7.已知cos(α-$\frac{π}{6}$)=-$\frac{1}{3}$,且α∈(0,π),则sinα等于( )| A. | $\frac{{2\sqrt{6}-1}}{6}$ | B. | $\frac{{2\sqrt{2}+\sqrt{3}}}{6}$ | C. | $\frac{{2\sqrt{6}+1}}{6}$ | D. | $\frac{{2\sqrt{2}-\sqrt{3}}}{6}$ |
分析 由已知求出sin(α-$\frac{π}{6}$),再由sinα=sin[($α-\frac{π}{6}$)+$\frac{π}{6}$],展开两角和的正弦求解.
解答 解:∵α∈(0,π),∴$α-\frac{π}{6}$∈($-\frac{π}{6},\frac{5π}{6}$),
又cos(α-$\frac{π}{6}$)=-$\frac{1}{3}$,∴sin(α-$\frac{π}{6}$)=$\sqrt{1-(-\frac{1}{3})^{2}}=\frac{2\sqrt{2}}{3}$,
∴sinα=sin[($α-\frac{π}{6}$)+$\frac{π}{6}$]=sin(α-$\frac{π}{6}$)cos$\frac{π}{6}$+(α-$\frac{π}{6}$)sin$\frac{π}{6}$
=$\frac{2\sqrt{2}}{3}×\frac{\sqrt{3}}{2}+(-\frac{1}{3})×\frac{1}{2}=\frac{2\sqrt{6}-1}{6}$.
故选:A.
点评 本题考查三角函数的化简求值,考查两角和与差的正弦,是基础的计算题.

练习册系列答案
相关题目
14.执行图示的程序框图,则输出的结果为( )
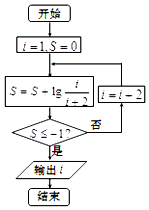

| A. | 7 | B. | 9 | C. | 10 | D. | 11 |
18.设命题p:?x∈R,x02>lnx,则¬p为( )
| A. | ?x0∈R,x02>lnx0 | B. | ?x0∈R,x02≥lnx0 | C. | ?x0∈R,x02<lnx0 | D. | ?x0∈R,x02≤lnx0 |
15.函数f(x)=x2+3x-4 的单调递增区间是( )
| A. | (-∞,$\frac{3}{2}$] | B. | [-$\frac{3}{2}$,+∞) | C. | [$\frac{3}{2}$,4) | D. | (-1,$\frac{3}{2}$] |
2.已知集合A={1,2,3},B={x|x2-4<0},则A∩B=( )
| A. | {1} | B. | {1,2} | C. | {2} | D. | {2,3} |
12. 从甲、乙两种玉米苗中各抽6株,分别测得它们的株高如图(单位:cm),根据以下数据可估计( )
从甲、乙两种玉米苗中各抽6株,分别测得它们的株高如图(单位:cm),根据以下数据可估计( )
 从甲、乙两种玉米苗中各抽6株,分别测得它们的株高如图(单位:cm),根据以下数据可估计( )
从甲、乙两种玉米苗中各抽6株,分别测得它们的株高如图(单位:cm),根据以下数据可估计( )| A. | 甲种玉米比乙种玉米不仅长得高而且长得整齐 | |
| B. | 乙种玉米比甲种玉米不仅长得高而且长得整齐 | |
| C. | 甲种玉米比乙种玉米长得高但长势没有乙整齐 | |
| D. | 乙种玉米比甲种玉米长得高但长势没有甲整齐 |
5.在(x-$\frac{2}{\sqrt{x}}$)6展开式中,常数项为( )
| A. | -192 | B. | -160 | C. | 60 | D. | 240 |