Question

20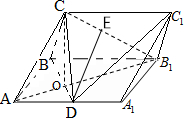．如图，在三棱柱ABC-A₁B₁C₁中，侧面ABB₁A₁为矩形，AB=1，AA₁=$\sqrt{2}$，D为AA₁的中点，BD与AB₁交于点O，CO⊥侧面ABB₁A₁，E为线段B₁C的中点．
（Ⅰ）证明：DE∥平面ABC；
（Ⅱ）若OC=OA，求二面角C-AB-A₁的余弦值．

Answer 1

分析 （Ⅰ）取BC的中点F，连接AF，EF，则EF平行且等于AD，证明：ADEF是平行四边形，可得AF∥DE，即可证明DE∥平面ABC；
（Ⅱ）作OM⊥AB，连接CM，则CM⊥AB，∠CMO为二面角C-AB-A₁的平面角，即可求二面角C-AB-A₁的余弦值．

解答 （Ⅰ）证明：取BC的中点F，连接AF，EF，则EF平行且等于AD，
∴ADEF是平行四边形，
∴AF∥DE，
∵DE?平面ABC，AF?平面ABC，
∴DE∥平面ABC；
（Ⅱ）解：作OM⊥AB，连接CM，则CM⊥AB，∠CMO为二面角C-AB-A₁的平面角，
侧面ABB₁A₁为矩形，AB=1，AA₁=$\sqrt{2}$，∴AO=$\frac{\sqrt{3}}{3}$=CO，OM=$\frac{\sqrt{2}}{3}$
∴CM=$\frac{\sqrt{5}}{3}$，
∴二面角C-AB-A₁的余弦值=$\frac{\sqrt{10}}{5}$．

点评 本题考查线面平行的判定，考查二面角的余弦值，考查学生分析解决问题的能力，属于中档题．