题目内容
12.已知曲线C:xy=1,先将曲线C作关于x轴的反射变换,再将所得图形绕原点顺时针旋转90°.(1)求连续两次变换所对应的变换矩阵M;
(2)求曲线C在TM作用下得到的曲线C′的方程.
分析 (1)利用矩阵的乘法,求连续两次变换所对应的变换矩阵M;
(2)求出变换前后坐标之间的关系,即可求曲线C在TM作用下得到的曲线C′的方程.
解答 解:(1)连续两次变换所对应的变换矩阵M=$[\begin{array}{l}{0}&{1}\\{-1}&{0}\end{array}]$$[\begin{array}{l}{1}&{0}\\{0}&{-1}\end{array}]$=$[\begin{array}{l}{0}&{-1}\\{-1}&{0}\end{array}]$;
(2)设曲线C上一点P(x,y)在M的作用下变为曲线C′上一点P′(x′,y′),则
$[\begin{array}{l}{x′}\\{y′}\end{array}]$=$[\begin{array}{l}{0}&{-1}\\{-1}&{0}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{-y}\\{-x}\end{array}]$,
∴x=-y′,y=-x′,
∵x′y′=1,
∴xy=1
点评 本题考查矩阵变换,考查方程思想,正确计算是关键.

练习册系列答案
相关题目
17.某程序框图如图所示,该程序运行结束时输出的S的值为( )


| A. | 1007 | B. | 1008 | C. | 2016 | D. | 3024 |
4.过点A(3,4)且与点B(-3,2)的距离最短的直线方程为( )
| A. | 3x-y-5=0 | B. | x-3y+9=0 | C. | 3x+y-13=0 | D. | x+3y-15=0 |
1. 元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=( )
元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=( )
 元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=( )
元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=( )| A. | $\frac{3}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{15}{16}$ | D. | $\frac{31}{32}$ |
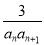 ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<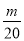 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.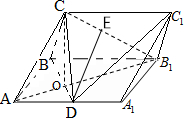 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,E为线段B1C的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,E为线段B1C的中点.