题目内容
已知向量a=(sin x,2cos x),b=(2sin x,sin x),设函数f(x)=a·b.
(1)求f(x)的单调递增区间;
(2)若将f(x)的图象向左平移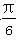 个单位,得到函数g(x)的图象,求函数g(x)在区间
个单位,得到函数g(x)的图象,求函数g(x)在区间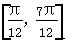 上的最大值和最小值.
上的最大值和最小值.
(1)f(x)=a·b=2sin2x+2sin xcos x=2× +sin 2x
+sin 2x
=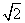 sin
sin +1,
+1,
 ∴0≤g(x)≤
∴0≤g(x)≤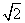 +1,
+1,
即g(x)的最大值为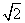 +1,最小值为0.
+1,最小值为0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则
,则 的值是______________
的值是______________ (
(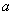 >0,
>0,  , 则
, 则 的图象为( )
的图象为( )
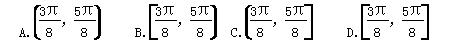
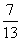 (0<α<π),则tan α=( )
(0<α<π),则tan α=( )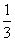 B.
B.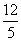 C.-
C.-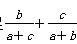 ≥1,则角A的范围是( )
≥1,则角A的范围是( )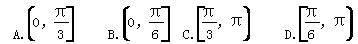
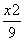 -
-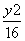 =1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到双曲线S的中心的距离为( )
=1的一个顶点和一个焦点,圆心M在双曲线S上,则圆心M到双曲线S的中心的距离为( )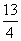 或
或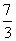 B.
B.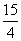 或
或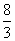 C.
C.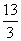 D.
D.