题目内容
在数列{an}中,已知a1=
,an=3an-1+3n-1(n≥2,n∈N*),则数列{an}的通项为an= .
| 7 |
| 2 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由首项结合数列递推式求出第二项和第三项,然后构造等差数列{
},求出其首项和公差,写出其通项公式,则数列{an}的通项公式可求.
| an-1 |
| 3n |
解答:
解:由a1=
,an=3an-1+3n-1,得
a2=3×
+8=
,
a3=3×
+28=
.
设
=xn+y,
则
.
解得:x=
,y=-
,λ=-1.
∴
=
n-
,
即数列{
}构成以
为首项,以
为公差的等差数列.
∴
=
+
(n-1)=
n-
.
∴an=(
n-
)•3n+1.
故答案为:(
n-
)•3n+1.
| 7 |
| 2 |
a2=3×
| 7 |
| 2 |
| 37 |
| 2 |
a3=3×
| 37 |
| 2 |
| 167 |
| 2 |
设
| an+λ |
| 3n |
则
|
解得:x=
| 10 |
| 9 |
| 5 |
| 18 |
∴
| an-1 |
| 3n |
| 10 |
| 9 |
| 5 |
| 18 |
即数列{
| an-1 |
| 3n |
| 5 |
| 6 |
| 10 |
| 9 |
∴
| an-1 |
| 3n |
| 5 |
| 6 |
| 10 |
| 9 |
| 10 |
| 9 |
| 5 |
| 18 |
∴an=(
| 10 |
| 9 |
| 5 |
| 18 |
故答案为:(
| 10 |
| 9 |
| 5 |
| 18 |
点评:本题考查了数列递推式,考查了利用构造法求数列的通项公式,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数f(x)=loga(x3-ax)(a>0且a≠1)在区间(-
,0)内单调递增,则实数a的取值范围是( )
| 1 |
| 4 |
A、[
| ||
B、[
| ||
C、[
| ||
| D、(1,3] |
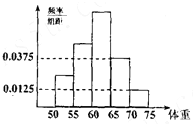 为了了解某市今年准备报考体育专业的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,则第2小组的频率为
为了了解某市今年准备报考体育专业的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,则第2小组的频率为 如图阴影部分是圆O的内接正方形,随机撒314粒黄豆,则预测黄豆落在正方形内的约
如图阴影部分是圆O的内接正方形,随机撒314粒黄豆,则预测黄豆落在正方形内的约