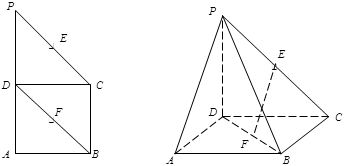题目内容
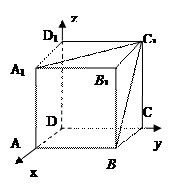
如图,边长为 的等边△
的等边△ 所在的平面垂直于矩形
所在的平面垂直于矩形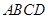 所在的平面,
所在的平面,  ,
, 为
为 的中点.
的中点.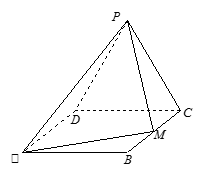
(1)证明: ;
;
(2)求二面角 的大小.
的大小.
(1)能利用已知建立空间直角坐标系,然后表示出点的坐标,进而证明 即可。
即可。
(2)
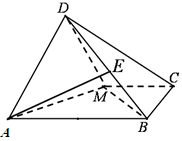
解析试题分析:证明:(1) 以 点为原点,分别以直线
点为原点,分别以直线 为
为 轴,
轴,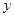 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系 ,依题意,
,依题意,
可得
 ,
,
∴ ,
, ,
,
∴ 即
即 ,
,
∴ .-----------6分
.-----------6分
(2)设 ,且
,且 平面
平面 ,则
,则 ,
,
即 ,
,
∴ ,即
,即 ,
,
取 ,得
,得 ,
,
取 ,显然
,显然 平面ABCD,
平面ABCD,
∴ ,
,
结合图形可知,二面角 为
为 . 12分
. 12分
考点:二面角,垂直的证明
点评:主要是考查了空间中的垂直的证明,以及二面角的平面角的求解运用,属于中档题。

练习册系列答案
相关题目
与直线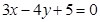 关于x轴对称的直线方程为( )
关于x轴对称的直线方程为( )
A. | B.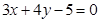 |
C. | D. |
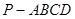 中,底面
中,底面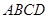 为菱形,
为菱形,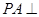 平面
平面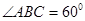 ,
, 分别是
分别是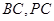 的中点.
的中点.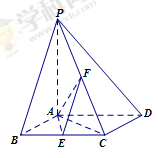
 平面
平面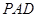 ;
; ,若
,若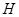 为
为 上的动点,
上的动点,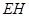 与平面
与平面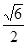 ,求二面角
,求二面角 的余弦值。
的余弦值。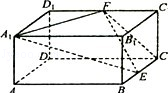
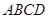 中,
中,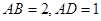 ,
,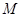 为
为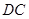 的中点. 将
的中点. 将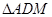 沿
沿 折起,使得平面
折起,使得平面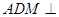 平面
平面 .
.
 ;
; 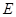 是线段
是线段 的中点,求二面角
的中点,求二面角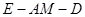 的余弦值.
的余弦值. 中,
中,
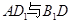 所成角;
所成角;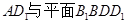 所成角的正弦.
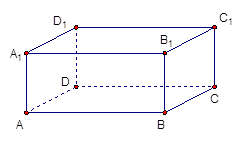
所成角的正弦.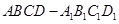 是正方体,其中
是正方体,其中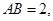
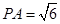
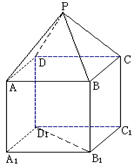
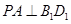 ;
;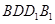 所成的锐二面角
所成的锐二面角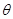 的余弦值;
的余弦值;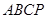 中,
中, ∥
∥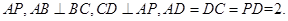
 分别是
分别是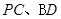 的中点,现将
的中点,现将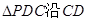 折起,使
折起,使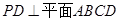 ,
,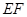 ∥平面
∥平面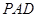 ;
; 到平面
到平面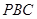 的距离.
的距离.