题目内容
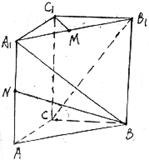
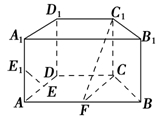
(本小题满分12分)如图, 在直角梯形 中,
中,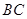 ∥
∥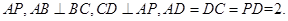
点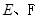 分别是
分别是 的中点,现将
的中点,现将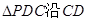 折起,使
折起,使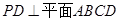 ,
,
(1)求证: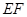 ∥平面
∥平面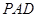 ;
;
(2)求点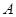 到平面
到平面 的距离.
的距离.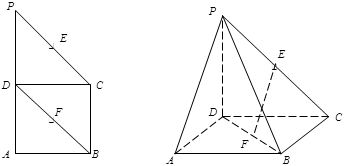
.解(1)连结AC, 底面ABCD是正方形,
底面ABCD是正方形, AC交BD于点F,且F是AC中点
AC交BD于点F,且F是AC中点
又点E为PC中点, EF∥PA,
EF∥PA,
 ∥平面PAD -------------5分
∥平面PAD -------------5分
(2)设点A到平面PBC的距离为h。 PD
PD 底面ABCD,
底面ABCD, PD
PD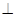 BC,
BC,
又DC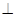 BC,DC
BC,DC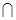 PC=D,
PC=D, BC
BC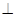 面PDC,
面PDC, BC
BC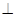 PC.
PC.
又由PD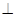 DC,PD=DC=2,得PC=
DC,PD=DC=2,得PC= ,
,

从而 --------------------8分
--------------------8分
另一方面,由PD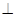 底面ABCD,AB
底面ABCD,AB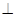 BC,且PD=AB=BC=2,得
BC,且PD=AB=BC=2,得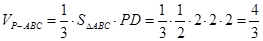
而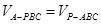 ,从而得:
,从而得: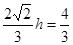 ,
,

即点A到平面PBC的距离为 . ----------12分
. ----------12分 

解析试题分析:(1)欲证EF∥平面APG,根据直线与平面平行的判定定理可知只需证AP与平面EFG内一直线平行即可,取AD中点M,连接FM、MG,由条件知EF∥DC∥MG,则E、F、M、G四点共面,再根据三角形中位线定理知MF∥PA,满足定理所需条件;
(2)利用等体积法来表示得到高度问题。
考点:本题主要是考查线面平行的判定定理和点到面的距离的求解运用。
点评:解决该试题的关键是通过利用三就爱哦行的中位线来得到平行线,然后借助于线线平行来得到线面平行的证明。同时利用等体积法求解高度问题。

练习册系列答案
相关题目
光线从点 发出,经过
发出,经过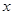 轴反射,再经过
轴反射,再经过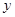 轴反射,最后光线经过点
轴反射,最后光线经过点 ,则经
,则经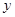 轴反射的光线的方程为( )
轴反射的光线的方程为( )
A. | B.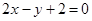 |
C.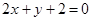 | D.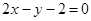 |


 ;
; 所成角的正弦值。
所成角的正弦值。 的等边△
的等边△ 所在的平面垂直于矩形
所在的平面垂直于矩形 所在的平面,
所在的平面,  ,
, 为
为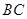 的中点.
的中点.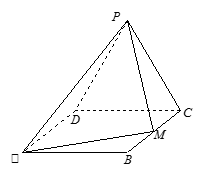
 ;
; 的大小.
的大小.
 BCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=
BCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
 边长都为2,且
边长都为2,且
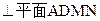 ,
, 的中点,
的中点,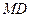
 。(2分)
。(2分) 的距离。(5分)
的距离。(5分)