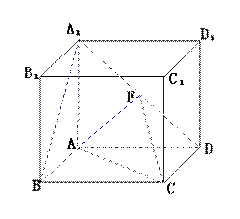
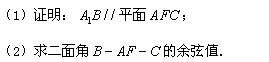题目内容
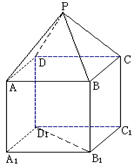
(理)如图,P—ABCD是正四棱锥,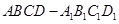 是正方体,其中
是正方体,其中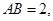
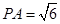
(1)求证: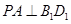 ;
;
(2)求平面PAD与平面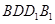 所成的锐二面角
所成的锐二面角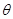 的余弦值;
的余弦值;
(1)以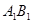 为
为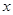 轴,
轴,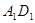 为
为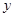 轴,
轴, 为
为 轴建立空间直角坐标系
轴建立空间直角坐标系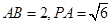 , ∴
, ∴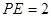 ∴
∴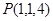 ∴
∴ 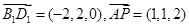
∴ 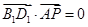 , 即
, 即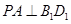 (2)
(2)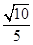
解析试题分析:以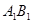 为
为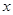 轴,
轴,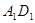 为
为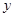 轴,
轴,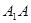 为
为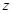 轴建立空间直角坐标系
轴建立空间直角坐标系
(1)证明:设E是BD的中点, P—ABCD是正四棱锥,
P—ABCD是正四棱锥,
∴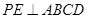
又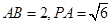 , ∴
, ∴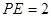 ∴
∴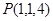
∴ 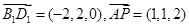
∴ 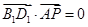 , 即
, 即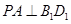 .
.
(2)解:设平面PAD的法向量是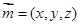 ,
, 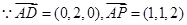
∴ 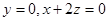 取
取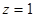 得
得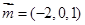 ,
,
又平面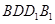 的法向量是
的法向量是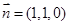
∴  , ∴
, ∴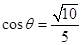 .
.
考点:直线垂直的判定及二面角的求解
点评:要证两直线垂直只需证明两直线的方向向量数量积为0,求二面角时首先找到两个半平面对应的法向量,求出法向量夹角,进而转化为平面角

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
如图,直线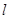 经过二、三、四象限,
经过二、三、四象限,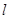 的倾斜角为
的倾斜角为 ,斜率为k,则 ( ).
,斜率为k,则 ( ).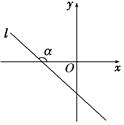
A.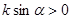 | B.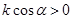 | C.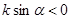 | D.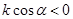 |
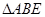 为等腰直角三角形,
为等腰直角三角形, ,且
,且 .
.
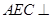 平面
平面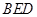 .
.
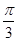 ,D、E分别为AA1、A1C的中点.
,D、E分别为AA1、A1C的中点.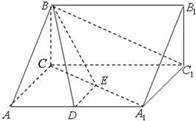
 的等边△
的等边△ 所在的平面垂直于矩形
所在的平面垂直于矩形 所在的平面,
所在的平面,  ,
, 为
为 的中点.
的中点.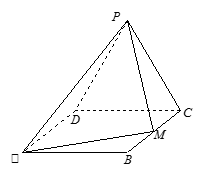
 ;
; 的大小.
的大小. 中,
中,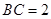 ,
, ,
,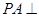 平面
平面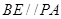 ,
,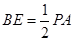 ,
,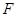 为
为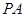 的中点.
的中点.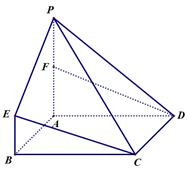
 平面
平面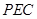 .
.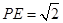 ,求平面
,求平面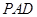 所成锐二面角的余弦值.
所成锐二面角的余弦值. BCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=
BCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
 的棱长为
的棱长为 ,点
,点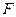 为
为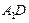 的中点.
的中点.