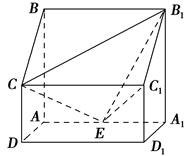
题目内容
如图,已知长方形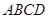 中,
中,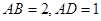 ,
,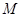 为
为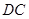 的中点. 将
的中点. 将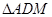 沿
沿 折起,使得平面
折起,使得平面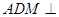 平面
平面 .
.
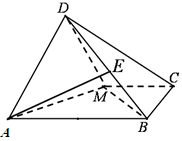
(I)求证: ;
;
(II)若点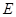 是线段
是线段 的中点,求二面角
的中点,求二面角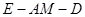 的余弦值.
的余弦值.
(I)详见解析;(II)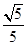 .
.
解析试题分析:(I)要证明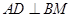 ,只需要建立适当坐标系,证明
,只需要建立适当坐标系,证明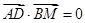 即可;(II)向量法求二面角的平面角首先分别求两个半平面的法向量,而平面
即可;(II)向量法求二面角的平面角首先分别求两个半平面的法向量,而平面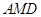 的法向量是显而以见的,所以只需求出平面
的法向量是显而以见的,所以只需求出平面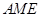 的法向量,利用法向量求得二面角的余弦值.
的法向量,利用法向量求得二面角的余弦值.
试题解析:(I):因为平面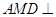 平面
平面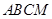 ,
,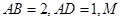 是
是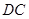 的中点,
的中点,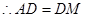 ,取
,取 的中点
的中点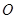 ,连结
,连结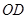 ,则
,则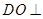 平面
平面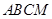 ,取
,取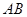 的中点
的中点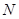 ,连结
,连结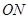 ,则
,则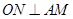 ,以
,以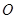 为原点如图建立空间直角坐标系,根据已知条件,得
为原点如图建立空间直角坐标系,根据已知条件,得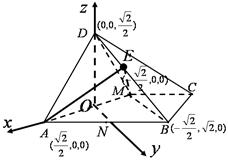
 ,
,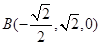 ,
,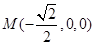 ,
, ,则
,则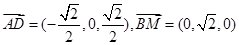 ,所以
,所以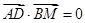 ,故
,故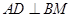 ;
;
(II)依题意得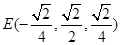 ,因为平面
,因为平面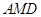 的一个法向量
的一个法向量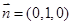 ,设平面
,设平面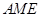 的一个法向量为
的一个法向量为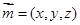 ,而
,而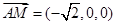 ,
,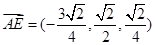 ,则
,则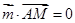 ,且
,且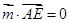 ,
,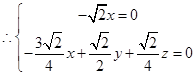 ,取
,取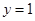 ,得
,得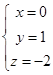 ,
,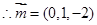 ,
,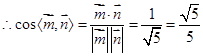 ,所以二面角
,所以二面角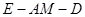 的余弦值为
的余弦值为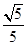 .
.
考点:1、空间向量垂直的坐标运算公式 ; 2、向量法求二面角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线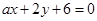 和直线
和直线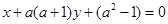 垂直,则
垂直,则 的值为( )
的值为( )
A. 或 或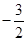 | B. 或 或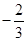 | C. 或 或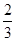 | D. 或 或 |
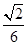 ,求线段AM的长.
,求线段AM的长.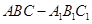 中,
中, ,
, ,
, 是
是 中点.
中点.
 平面
平面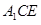 ;
; 与平面
与平面
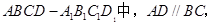


 ;
; 所成角的正弦值。
所成角的正弦值。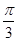 ,D、E分别为AA1、A1C的中点.
,D、E分别为AA1、A1C的中点.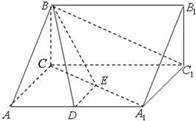
 的等边△
的等边△ 所在的平面垂直于矩形
所在的平面垂直于矩形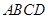 所在的平面,
所在的平面,  ,
, 为
为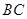 的中点.
的中点.
 ;
; 的大小.
的大小. BCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=
BCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.