题目内容
13.已知函数f(x)=|x-a|,g(x)=$\frac{1}{x}$,若方程f(x)=g(x)-a有且只有一个实数根,则实数a的取值集合为(-1,+∞).分析 把方程f(x)=g(x)-a有且只有一个实数根,转化为|x-a|+a=$\frac{1}{x}$有且只有一个实数根,令h(x)=|x-a|+a,t(x)=$\frac{1}{x}$.分类作出两函数图象即可求得实数a的取值集合.
解答 解:方程f(x)=g(x)-a有且只有一个实数根,
即|x-a|=$\frac{1}{x}$-a有且只有一个实数根,
也就是|x-a|+a=$\frac{1}{x}$有且只有一个实数根,
令h(x)=|x-a|+a,t(x)=$\frac{1}{x}$.
若a=0,则h(x)=|x|,作出函数图象如图1:
方程f(x)=g(x)-a有且只有一个实数根;
若a>0,函数h(x)是把函数y=|x|的图象向右向上平移a个单位得到,
作出函数h(x)与t(x)的图象如图2:
对于任意a>0,方程f(x)=g(x)-a有且只有一个实数根;
若a<0,函数h(x)是把函数y=|x|的图象向左向下平移|a|个单位得到,
作出函数h(x)与t(x)的图象如图3:
要使方程f(x)=g(x)-a有且只有一个实数根,则-1<a<0.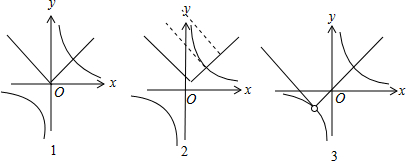
综上,实数a的取值集合为(-1,+∞).
故答案为:(-1,+∞).
点评 本题考查根的存在性与根的个数判断,考查数学转化思想方法与数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
1.已知点A(-1,-2),B(1,-1),C(x,2),若A、B、C三点共线,则x的值为( )
| A. | -4 | B. | -3 | C. | 2 | D. | 7 |
8.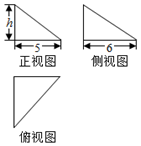 如图所示,三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的表面积(单位:cm2)等于( )
如图所示,三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的表面积(单位:cm2)等于( )
 如图所示,三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的表面积(单位:cm2)等于( )
如图所示,三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的表面积(单位:cm2)等于( )| A. | 75π | B. | 77π | C. | 65π | D. | 55π |
18.已知tanα=2,α∈(0,π),则cos($\frac{9π}{2}$+2α)等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{5}$ | C. | -$\frac{2}{5}$ | D. | -$\frac{4}{5}$ |
5.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{64}{3}$ | B. | 32 | C. | 64 | D. | $\frac{32}{3}$ |
