题目内容
已知轴对称平面五边形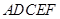 (如图1),
(如图1),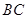 为对称轴,
为对称轴,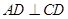 ,
,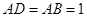 ,
,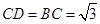 ,将此图形沿
,将此图形沿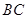 折叠成直二面角,连接
折叠成直二面角,连接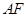 、
、 得到几何体(如图2).
得到几何体(如图2).

(Ⅰ)证明: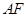 ∥平面
∥平面 ;
;
(Ⅱ)求二面角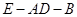 的余弦值.
的余弦值.
(Ⅰ)详见解析;(Ⅱ)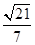 .
.
解析试题分析:(Ⅰ)主要利用空间向量、线线平行可证线面平行;(Ⅱ)主要利用平面的法向量来求二面角的平面角.
试题解析:(Ⅰ) 以B为坐标原点,分别以射线BF、BC、BA为x轴、 y轴、z轴的正方向建立如图所示的坐标系.
以B为坐标原点,分别以射线BF、BC、BA为x轴、 y轴、z轴的正方向建立如图所示的坐标系.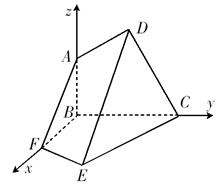
由已知与平面几何知识得,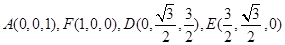 ,
,
∴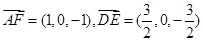 ,
,
∴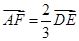 ,∴AF∥DE,
,∴AF∥DE,
又 平面
平面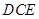 ,且
,且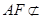 平面
平面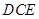
∴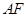 ∥平面
∥平面
(Ⅱ)由(Ⅰ)得 四点共面,
四点共面,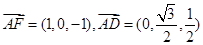 ,
,
设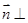 平面
平面 ,
, ,则
,则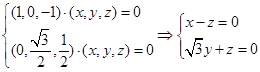 ,
,
不妨令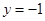 ,故
,故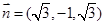 ,
,
由已知易得平面ABCD的一个法向量为 ,
,
∴ ,∴二面角E-AD-B的余弦值为
,∴二面角E-AD-B的余弦值为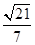 .
.
考点:立体几何线面平行的证明、二面角的求解,考查学生的空间想象能力和空间向量的使用.

练习册系列答案
相关题目
 中,侧面
中,侧面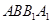 为矩形,
为矩形,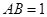 ,
,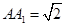 ,
,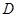 为
为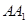 的中点,
的中点,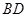 与
与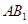 交于点
交于点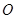 ,
, 侧面
侧面
 ;
; ,求三棱锥
,求三棱锥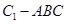 的体积.
的体积.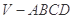 中,底面
中,底面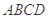 是正方形,侧面
是正方形,侧面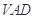 是正三角形,平面
是正三角形,平面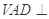 底面
底面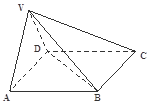
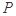 为线段VC的中点,求证:
为线段VC的中点,求证: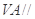 平面
平面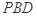 ;
;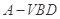 的体积
的体积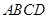 是正方形,
是正方形,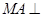 平面
平面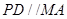 ,
,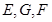 分别为
分别为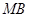 ,
,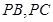 的中点,且
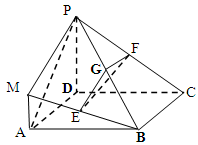
的中点,且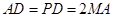 .
.
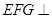 平面
平面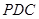 ;
;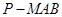 与四棱锥
与四棱锥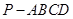 的体积之比.
的体积之比.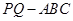 中,
中,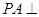 平面
平面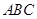 ,平面
,平面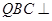 平面
平面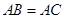 ,
,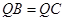 .
.
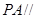 平面
平面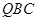 ;
;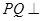 平面
平面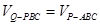 .
.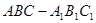 ,底面三角形
,底面三角形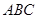 为正三角形,侧棱
为正三角形,侧棱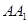
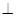 底面
底面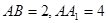 ,
,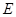 为
为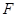 为
为 中点.
中点.
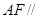 平面
平面 ;
; 到平面
到平面 BQ并说明理由.
BQ并说明理由.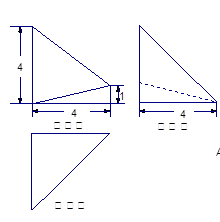
 中,
中,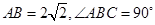 ,点
,点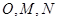 分别为线段
分别为线段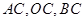 的中点,将
的中点,将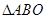 和
和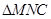 分别沿
分别沿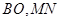 折起,使二面角
折起,使二面角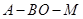 和二面角
和二面角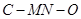 都成直二面角,如图(2)所示。
都成直二面角,如图(2)所示。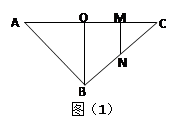

 面
面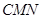 ;
;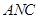 与平面
与平面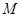 到平面
到平面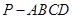 中,
中,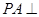 平面
平面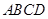 ,四边形
,四边形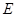 ,
,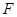 分别是
分别是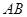 ,
,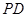 的中点.若
的中点.若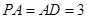 ,
,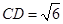 。
。
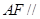 平面
平面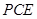 ;
; 平面
平面