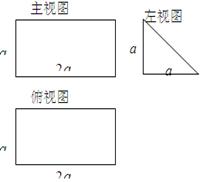
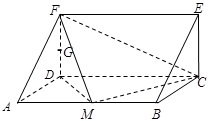题目内容
如图(1),在等腰直角三角形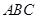 中,
中,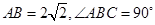 ,点
,点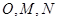 分别为线段
分别为线段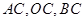 的中点,将
的中点,将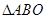 和
和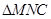 分别沿
分别沿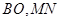 折起,使二面角
折起,使二面角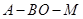 和二面角
和二面角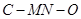 都成直二面角,如图(2)所示。
都成直二面角,如图(2)所示。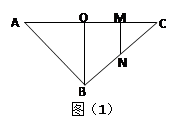

(1)求证: 面
面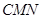 ;
;
(2)求平面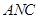 与平面
与平面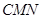 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)求点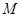 到平面
到平面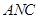 的距离。
的距离。
(1)利用线线平行证明线面平行,(2) (3)
(3)
解析试题分析:(1) 面
面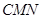 ,
, 面
面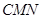
且 ,
, ,又
,又
(2)分别以 为
为 轴建立坐标系,则
轴建立坐标系,则

 ,
, ,设平面
,设平面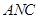 的法向量为:
的法向量为: ,则有
,则有 ,令
,令 ,而平面
,而平面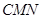 的法向量为:
的法向量为:

(3) ,由(2)知平面
,由(2)知平面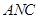 的法向量为:
的法向量为: ,
,
考点:本题考查了空间中的线面关系
点评:此类问题常考查空间中平行关系与垂直关系的证明以及几何体体积的计算,这是各类考试的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
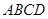 与直角梯形
与直角梯形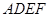 所在平面互相垂直,
所在平面互相垂直,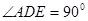 ,
, ,
,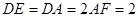 .
.
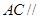 平面
平面 ;
;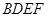 的体积.
的体积.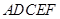 (如图1),
(如图1),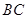 为对称轴,
为对称轴,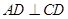 ,
,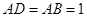 ,
,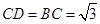 ,将此图形沿
,将此图形沿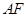 、
、 得到几何体(如图2).
得到几何体(如图2).

 ;
; 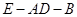 的余弦值.
的余弦值.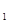 B
B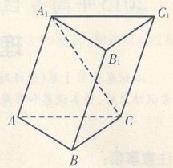
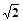 ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。


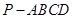 中,底面
中,底面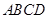 为矩形,
为矩形,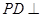 平面
平面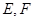 分别是
分别是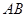 和
和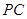 的中点.
的中点.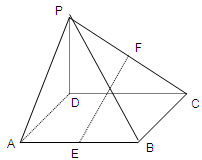
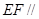 平面
平面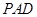 ;
;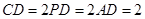 , 四棱锥
, 四棱锥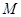 、
、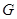 分别是
分别是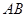 、
、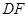 的中点.
的中点.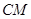
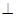 平面
平面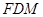
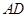 上(含
上(含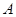 、
、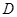 端点)确定一点
端点)确定一点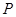 ,使得
,使得
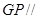 平面
平面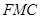 ,并给出证明;
,并给出证明;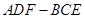 内自由飞,求它飞入几何体
内自由飞,求它飞入几何体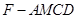 内的概率.
内的概率.