题目内容
在空间几何体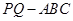 中,
中,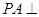 平面
平面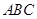 ,平面
,平面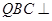 平面
平面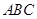 ,
,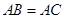 ,
,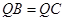 .
.
(I)求证: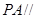 平面
平面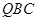 ;
;
(II)如果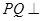 平面
平面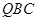 ,求证:
,求证: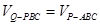 .
.
(Ⅰ)详见解析;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)利用平面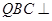 平面
平面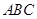 得到平面
得到平面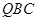 内一条直线与平面
内一条直线与平面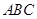 垂直,然后利用直线与平面垂直的性质定理得到该直线与
垂直,然后利用直线与平面垂直的性质定理得到该直线与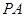 平行,进而证明
平行,进而证明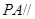 平面
平面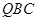 ;(Ⅱ)利用已知条件确定三棱锥
;(Ⅱ)利用已知条件确定三棱锥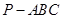 和
和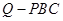 的高与底面积,及三棱锥
的高与底面积,及三棱锥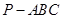 和
和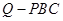 中相应的边长之间的等量关系,然后将三棱锥
中相应的边长之间的等量关系,然后将三棱锥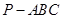 和
和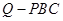 的体积用对应的边长进行表示,两者进行比较从而得出
的体积用对应的边长进行表示,两者进行比较从而得出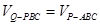 .
.
试题解析:(I)如图,取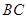 中点
中点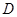 ,连
,连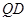 ,
,
由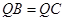 得
得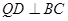 ,
,
∵平面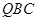 ⊥平面
⊥平面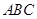 , ∴
, ∴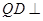 平面
平面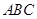 , 2分
, 2分
又∵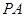 ⊥平面
⊥平面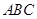 ,∴
,∴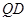 ∥
∥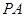 , 4分
, 4分
又∵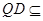 平面
平面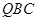 ,∴
,∴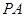 ∥平面
∥平面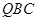 . 6分
. 6分
(Ⅱ)连接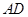 ,则
,则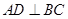 .
.
∵平面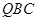 ⊥平面
⊥平面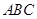 ,面
,面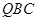 ∩面
∩面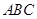
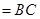 ,∴
,∴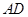 ⊥平面
⊥平面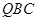 .
.
又∵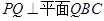 ,∴
,∴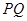 ∥
∥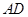 . 8分
. 8分
又由(Ⅰ)知,四边形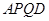 是矩形,
是矩形,
∴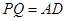 ,
,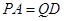 . 10分
. 10分
∴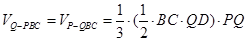 ,
,
而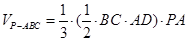 ,则
,则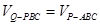 . 12分
. 12分
考点:直线与平面平行、几何体的体积

练习册系列答案
相关题目

 ,求三棱锥B1-A1DC的体积.
,求三棱锥B1-A1DC的体积.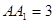 .
.

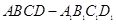 中,
中, ,点E是AB的中点.
,点E是AB的中点.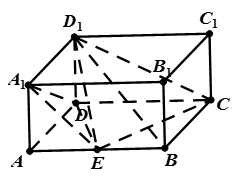
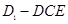 的体积;
的体积;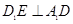 ;
; 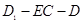 的正切值.
的正切值.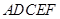 (如图1),
(如图1),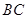 为对称轴,
为对称轴,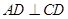 ,
,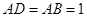 ,
,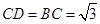 ,将此图形沿
,将此图形沿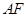 、
、 得到几何体(如图2).
得到几何体(如图2).

 ;
; 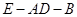 的余弦值.
的余弦值. 是
是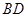 的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.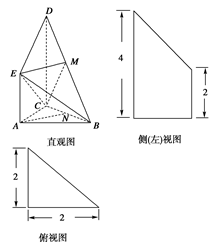
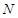 是
是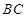 的中点,求证:
的中点,求证: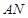 ∥平面
∥平面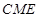 ;
;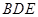 ⊥平面
⊥平面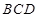 .
. B
B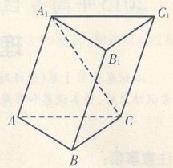

 平面PBD;
平面PBD;